ответ:
выведем полярное уравнение для отличного от окружности эллипса, параболы или правой ветви гиперболы. для этого совместим полюс полярной системы координат с левым фокусом эллипса (правым фокусом гиперболы) или единственным фокусом параболы, а полярную ось направим перпендикулярно директрисе d, соответствующей фокусу. обозначим через f, р и ε соответственно фокус, фокальный параметр и эксцентриситет кривой. пусть м — произвольная точка кривой, мf = r— полярный радиус точки м, φ — ее полярный угол. тогда
─ полярное уравнение эллипса, отличного от окружности, параболы, правой ветви гиперболы.
для левой ветви гиперболы
пошаговое объяснение:
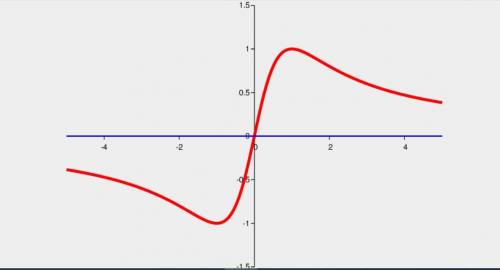
Дана функция y = 2x/(x² + 1.
Функция нечетная.
Условия для точек разрыва : x² + 1 = 0, x² = -1.
Точки разрыва : нет.
Корни функции (точки пересечения с осью абсцисс x) : x = 0.
Вычисление y′ : y′=2⋅1(x²+1)−x(2x)(x²+1)2=2⋅1−x²(x²+1)2=−2(x−1)(x+1)(x2+1)2
Первая производная : y′=−2(x−1)(x+1)/(x²+1)²
Условия для стационарных точек : −2(x−1)(x+1)=0
Стационарные точки : х1=−1, х2=1
Вторая производная : y′′=4x(x²−3)/(x²+1)³
Условия для критических точек : 4x(x²−3)=0
Критические точки : х1=−√3, х2=√3, х3=0
Асимптота на обоих ±∞ линия y=0.