1. - е.
2. - а.
3. -
Пошаговое объяснение:
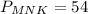см
1. Боковая сторона на 6 см больше основания.
Пусть MN = х см - основание, тогда MK = KN = (х + 6) см - боковая сторона.
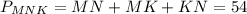см
x + (x + 6) + (x + 6) = 54
3x + 12 = 54
3x = 54 - 12
3x = 42
x = 14
MN = 14 см
MK = KN = 14 + 6 = 20 см
Соответствует варианту e.
2. Основание на 3 см больше боковой стороны.
Пусть MN = х см - основание, тогда MK = KN = (х - 3) см - боковая сторона.
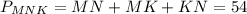см
x + (x - 3) + (x - 3) = 54
3x - 6 = 54
3x = 54 + 6
3x = 60
x = 20
MN = 20 см
MK = KN = 20 - 3 = 17 см
Соответствует варианту a.
3. Основание на 2 см меньше боковой стороны.
Пусть MN = х см - основание, тогда MK = KN = (х + 2) см - боковая сторона.
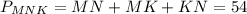см
x + (x + 2) + (x + 2) = 54
3x + 4 = 54
3x = 54 - 4
3x = 50
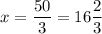
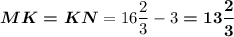см
см
Не соответствует ни одному из предложенных вариантов.
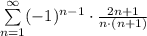
Исследуем этот ряд на абсолютную сходимость.
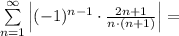
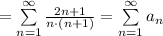
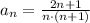
Рассмотрим ряд
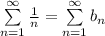
Используем предельный признак сравнения:
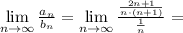
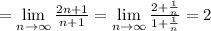
Значит ряды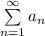 
и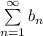 
сходятся или расходятся одновременно, но ряд
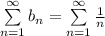
это гармонический ряд, который расходится. Значит и ряд
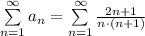
расходится.
Исследуем данный в задании ряд на условную сходимость. Используем признак Лейбница. Ряд знакочередующийся.
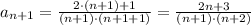
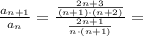
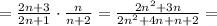
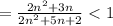
т.к.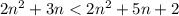 
⇔ 
⇔ 
.
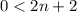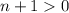То есть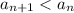 
.
То есть последовательность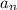 
монотонно убвывает.
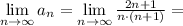
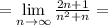
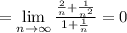
То есть последовательность 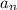монотонно убвывает и стремится к нулю. Итак, по признаку Лейбница, исходный ряд сходится.
ответ. Сходится условно.
Длина 3-8 См
Длина 4-3 СМ.
Если надо с мм скажи))