Прямая проходящая через точки A, B имеет уравнение:
y=ax+t, подставим координаты точек чтобы найти уравнение в явном виде.
6=a·o+t ⇒ t=6; 0=a·4+t ⇒ a=-6/4=-1,5
y = -1,5x+6
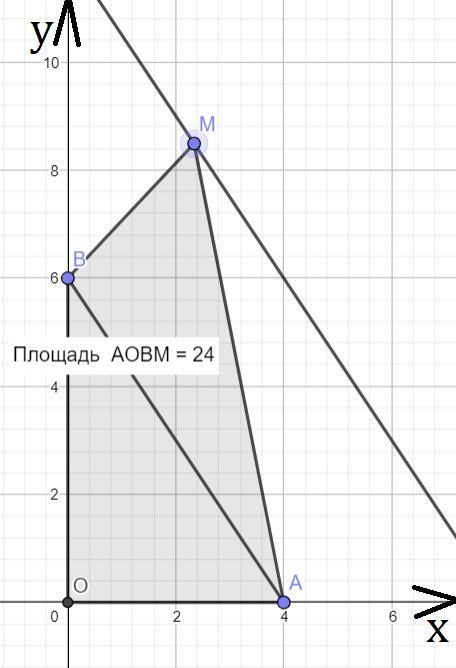
Исходя из последовательности вершин четырёхугольника, получаем, что координаты M(x;y) удовлетворяют неравенству y≥-1,5x+6.
Заметим, что S(AOBM) = S(AOB)+S(BMA), при этом S(AOBM)=24, S(AOB)=AO·OB/2=12.
Тогда S(BMA)=12.
Поскольку площадь треугольника постоянная и длина стороны AB тоже. То высота опущенная из M на AB должна быть постоянной, откуда M лежит на прямой параллельной AB. Тогда угол наклона k равен углу наклона прямой проходящей через точки A, B.
k = -1,5
ответ: -1,5.
ответ: y= -1,5; 8
( 12 у + 18) (1,6 – 0,2у) = 0.
Нулем ( ноль произведением является тогда, когда хотя бы один множитель- 0) является либо первая часть уравнения, либо вторая, либо обе они одновременно.
Предположим, что первая часть=0
Тогда 12y должны быть равны -18 (18+(-18)=0),
Тогда у = -18:12= -1,5
Подставляем значение у во вторую часть уравнения
1,6 - 0,2*(-1,5)= 1,6 - (-0,3)= 1,9
1,9 не равно 0, значит обе части уравнения нулем не являются.
Ну и разбираем последний вариант, когда 1,6 - 0,2у=0;
Тогда 0,2у должен равнятся 1,6 ( 1,6:0,2= 8)
Тогда у =8
Почему так: неважно, какие цифры были на первых шести местах, позиции цифр номера телефона не зависят друг от друга. Поэтому надо посчитать вероятность того, что если из 10 цифр попытаемся угадать цифру, она окажется верной. А она равна очевидно 1/10.