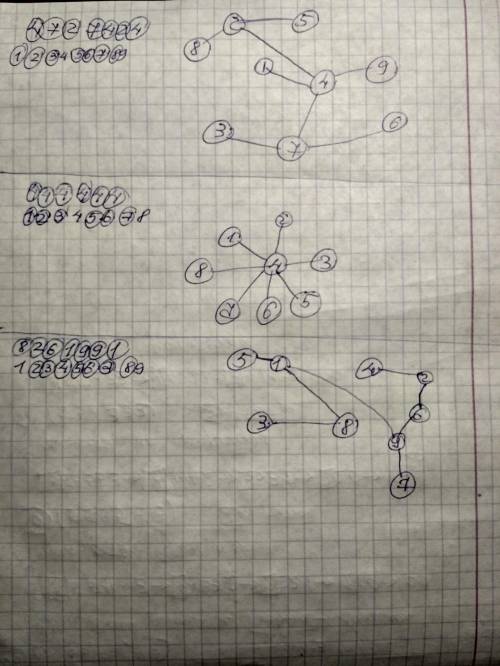
Задание 1
ответ в приложении
Задание 2
Тут, очевидно, опечатка, k<n. В дереве на n вершинах не может быть вершины степени n.
n=1:
k=0 - одно дерево, состоящее из одной вершины.n=2:
k=0 => граф не связный => не деревоk=1 => одно дерево, состоящее из одного ребраn>2:
k=0 => граф не связный => не деревоk>0 => Тогда каждому дереву поставим в соответствие код Прюфера. Его длина - n-2. Т.к. вершина 1 имеет степень k, то встречается в нем k-1 раз. Тогда для остальных n-1 вершин остается n-2-(k-1)=n-k-1 мест. Тогда всего таких кодов Прюфера, и, следовательно, деревьев,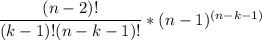
Задание 3
Найти количество деревьев с n вершинами, имеющими вершину степени n-2.
Зафиксируем номер этой вершины. Тогда в коде Прюфера она встречается n-3 раз. Тогда для остальных n-1 вершин остается n-2-(n-3)=1 место. Кол-во выбора номера вершины степени n-2 из n равно n. Тогда искомое число деревьев равно 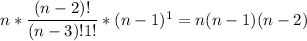
Дано:
D=10√3
Найти а - ребро куба.
Решение.
Пусть а (см) - ребро куба
1) В основании куба будет квадрат со стороной а (см). Найдём диагональ этого основания по теореме Пифагора.
а² + а² = d²
d² = 2a²
d=a√2
2) Диагональ основания, высота куба и диагональ всего куба образуют прямоугольный треугольник, в котором:
а - это катет
a√2 - второй катет
10√3 - диагональ
С теоремы Пифагора получаем уравнение:
a² + (a√2)² = (10√3)²
a² + 2a² = 100·3
3a² = 300
a² =300 : 3
a² = 100
a₁ = √100 = 10 см
а₂ = -√100 = - 10 < 0
ответ: 10 см