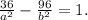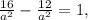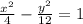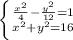1) 1/30 · (580 + 320) = 1/30 · 900 = 900 : 3 = 300
2) (637 - 274) : 1/2 = 363 · 2 = 726
4. Число делится на 3, если сумма его цифр кратна 3
9+6+4=19-сумма цифр
19 = 18 (кратно 3) + 1 в остатке
Проверяем: 964 : 3 =321 (ост. 1)
5. 1 м = 100 см
569 см = (569 : 100) м = 5,69 м
5,69 м · 1000 = 5690 м
6. 385000 м : 100 = 3850 м
1 м = 10 дм
3850 м = (3850 · 10) дм = 38500 дм
7. 350 · 5 = (300 + 50) · 5 = 300 · 5 + 50 · 5 = 1500 + 250 = 1750
8. Р = 4а = 360 см - периметр квадрата
а = 360 : 4 = 90 см = 9 дм - длина стороны квадрата
S = a² = 9 · 9 = 81 дм² - площадь квадрата
9. 1 м = 100 см; 1 см = 10 мм
5 м 650 мм = (5 · 100) см + (650 : 10) см = 500 см + 65 см = 565 см
10. 1 ч = 60 мин
420 мин = (420 : 60) ч = 7 ч
 .
.