Пошаговое объяснение:
1) Почему автор не учитывает ОДЗ, а именно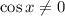 
и 
?
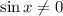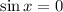или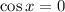 
не являются решениями:
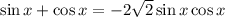
Пусть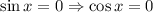 
- невозможно
Пусть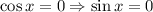 
- невозможно
2) Ваш ответ, к сожалению, неверен.
Например, возьмём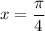 
:
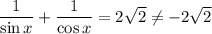
Во-первых, Вы возводите уравнение в квадрат, это неэквивалентное преобразование - так Вы легко можете найти дополнительные неверные решения. Например, если неверное равенство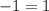 
возвести в квадрат, то оно станет верным 
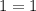. Поэтому при таком решении обязательно в самом конце подставить все найденные решения в исходное уравнение и отобрать из них верные.
Во-вторых, основная Ваша ошибка находится в пункте 6:
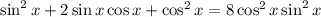
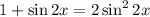, а у вас справа просто 
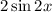- без квадрата.
3) Приложенное решение, как минимум, тоже имеет опечатку:
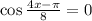
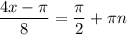- там же 
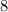в знаменателе упущена
В остальном, я считаю, что приложенное решение верное.
у км/ч - скорость течения
30 мин=0,5 ч
5(х+у)+3(х-у)=244
2(х+у)+0,5(х-у)=78
5х+5у+3х-3у=244
2х+2у+0,5х-0,5у=78
8х+2у=244
2,5х+1,5у=78
4х+у=122
2,5х+1,5у=78
у=122-4х
2,5х+1,5(122-4х)=78
у=122-4х
2,5х+183-6х=78
у=122-4х
3,5х=105
у=122-4х
х=30
у=122-4*30
х=30
у=2(км/ч) - скорость течения
х=30(км/ч) - скорость парохода