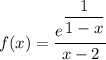1. Рассмотрим точку 11. Тут явно разрыв, так как функция не определена
2. Вычислим односторонние пределы
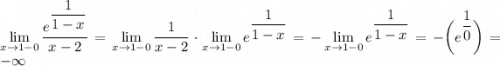
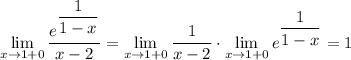
То есть функция сначала ушла в -∞ а затем резко появилась в 1
это разрыв второго рода
2. Рассмотрим точку 21. Тут опять разрыв, смотрим какой
2. Вычислим односторонние пределы
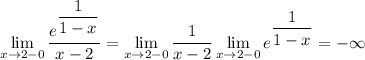
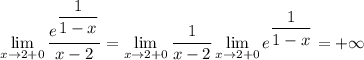
То есть функция сначала уходит в -∞ а потом выходит из +∞
В этой точке тоже разрыв второго рода
это точки - края определения кусочно-заданой функции
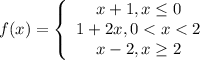
точки: х = 0 и х = 2
1. Точка х = 01. В данной точке существует значение функции?
Да,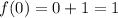 
2. Выполняется равенство односторонних пределов?
Да,
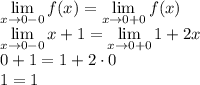
3. Существует ли предел в этой точке и конечен ли он?
Да,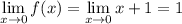 
1. В данной точке существует значение функции?
Да,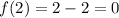 
2. Выполняется равенство односторонних пределов?
Нет,
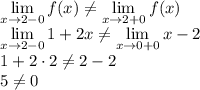
В этой точке функция терпит разрыв первого рода, а значит не является непрерывной
6,43
6,302
как сравнить -по дробной части
6,302 и 6,430
добавляем 0 и сравниваем 430 больше ,чем 302
6,7 и 6,43
добавляем 0 и сравниваем
6,70 и 6,43 - 70 больше ,чем 43