Большая сторона первоначального прямоугольника x.
Есть два возможный варианта: 1) прямоугольник разрезали по меньшей стороне; 2) прямоугольник разрезали по большей стороне. Рассмотрим их оба:
1) пусть одна сторона первого прямоугольника y, тогда вторая 6-y. Вторые стороны у обоих x.
Площади: xy кв.ед. у первого, x·(6-y) кв.ед. у второго. У первого в 3 раза больше:
xy = 3x·(6-y)
Периметры: (x+y)·2 у первого, (x+6-y)·2 у второго. У первого в 2 раза больше:
(x+y)·2 = 2·(x+6-y)·2
Составим и решим систему уравнений:

Большая сторона первоначального прямоугольника 1,5.
2) пусть одна сторона первого прямоугольника y, тогда вторая x-y. Вторые стороны у обоих 6.
Площади: 6y кв.ед. у первого, 6(x-y) кв.ед. у второго. У первого в 3 раза больше:
6y = 3·6(x-y)
Периметры: у первого (y+6)·2, у второго (x-y+6)·2, у первого в 2 раза больше:
(y+6)·2 = 2·(x-y+6)·2.
Составим и решим систему уравнений:
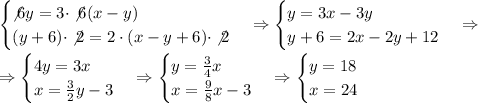
Большая сторона первоначального прямоугольника 24.
ответ: 1,5 или 24.
пошаговое объяснение:
пусть х количество десятков, у кол. единиц в числе, тогда двузначное число можно записать так:
10 х+у, а после перестановки оно будет вот таким:
10 у+х, сказано, что оно уменьшится на 16. составим уравнение
10 х+у=10 у+х+16
выразим х через у
9 х=9 у+16
х = (9 у+16) / 9
у может быть любым числом от 0 до 9
проверяем:
если у=0 х=16/9 чего не может быть, те это количество десятков и число должно получится от 1 до9
если у=1 х=34/9 не может быть
и так далее
при у=7 х=9
те искомое число 97
а число 79 на 16 меньше.
1) искомая_вероятность = (количество_кратных_4)/(всевозможное_количество_чисел).
2) количество_кратных_4 получается, когда выпадет 4, 8, 12 и 16. Так как чисел немного, можно расписать их:
выпавшая сумма 4: 112, 121 и 211 - 3 случая, то есть когда на кубиках были цифры 1,1 и 2, причём в разных порядках. Аналогично считается и для следующих комбинаций/сумм.
выпавшая сумма 8: (1,3и4 - 6 случаев, 1,2и5 - 6 случаев, 1,1и6 - 3 случая, 2,2и4- 3 случая, 2,2и3 - 3 случая, 3,1,3 - 3 случая) - итого 6+6+3+3+3+3=24 случая.
выпавшая сумма 12: (1,5,6 - 6 случаев, 2,5,5 - 3 случая, 2,6,4 - 6 случаев, 3,6,3 - 3 случая, 3,5,4 - 6 случаев, 4,4,4 - 1 случай) - итого 6+3+6+3+6+1=25 случаев.
выпавшая сумма 16: (4,6,6 - 3 случая, 5,5,6 - 3 случая) - итого 6 случаев.
3) Всевозможное количество сумм может выпасть 6³=216-ю
4) Искомая вероятность=(3+24+25+6)/216=58/216=29/108≈0,26(851)