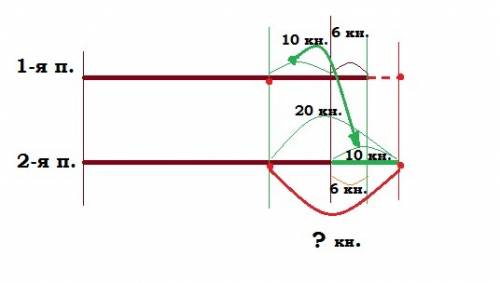
было на 1-ой полке ---- ? кн, но на 6 кн. > 2-ой
переставили с 1-ой на 2-ю ----- 10 кн.
стала разница ----- ? кн
Решение.
1. А р и ф м е т и ч е с к и й с п о с о б.
Перестановка и перекладывание дает двойную разницу по сравнению с числом перекладываемых предметов, т.к. складываем уменьшение и прибавление.
10 * 2 = 20 (кн) ----- на столько на второй стало бы больше при перестановке, если бы раньше было равно.
20 - 6 = 14 (кн.) ---- действительная разница, т.к. раньше на первой полке было больше.
ответ: На 14 книг на второй полке стало больше, чем на первой2. А л г е б р а и ч е с к и й с п о с о б
Х кн. ----- число книг на первой полке сначала
(Х - 6) кн. ---- число книг на второй полке сначала
(Х - 10) кн. ---- осталось на первой полке
((Х - 6) + 10) = (Х + 4) кн. --- стало на второй полке
(Х + 4) - (Х - 10) = Х + 4 - Х + 10 = 14 (кн) ---- стала разница: на второй больше.
ответ: на 14 книг стало больше на второйВс схематическая модель дана в приложении.
Выражение для решения: 10 - 6 + 10 = 14
было на 1-ой полке ---- ? кн, но на 6 кн. > 2-ой
переставили с 1-ой на 2-ю ----- 10 кн.
стала разница ----- ? кн
Решение.
1. А р и ф м е т и ч е с к и й с п о с о б.
Перестановка и перекладывание дает двойную разницу по сравнению с числом перекладываемых предметов, т.к. складываем уменьшение и прибавление.
10 * 2 = 20 (кн) ----- на столько на второй стало бы больше при перестановке, если бы раньше было равно.
20 - 6 = 14 (кн.) ---- действительная разница, т.к. раньше на первой полке было больше.
ответ: На 14 книг на второй полке стало больше, чем на первой2. А л г е б р а и ч е с к и й с п о с о б
Х кн. ----- число книг на первой полке сначала
(Х - 6) кн. ---- число книг на второй полке сначала
(Х - 10) кн. ---- осталось на первой полке
((Х - 6) + 10) = (Х + 4) кн. --- стало на второй полке
(Х + 4) - (Х - 10) = Х + 4 - Х + 10 = 14 (кн) ---- стала разница: на второй больше.
ответ: на 14 книг стало больше на второйВс схематическая модель дана в приложении.
Выражение для решения: 10 - 6 + 10 = 14

Не менее 2-х брюнетов - это 2 или 3 из трех случайных.
Вероятность брюнета - p = 0.2, q = 1 - p = 0.8.
Событие Р(А) = p³ + 3*p²q = 0.2³ + 3*0.2²*0.8 = 0.008 + 0,096 = 0.176 = 17,6% - ОТВЕТ
2)
Два шатена и блондин p(ш) = 0.4, р(б) = 0,3. Блондин - один из трех - три варианта.
P(A) = 3*p₃²*p₂ = 3*0.4²*0.3 = 3*0.16*0.3 = 0.144 = 14,4% - ОТВЕТ
3)
Вычислим противоположное событие - все три рыжих. q= 0.9
Q(A) = q³ = 0.729 - все три
P(A) = 1 - 0.729 = 0.271 = 27.1% - хотя бы один рыжий - ОТВЕТ