частное x³ + 2x² + 6x + 2, остаток 5
Пошаговое объяснение:
x⁴ + 2x² - 10x + 1 разделить на x - 2 по схеме Горнера:
В нашем случае x - a = x - 2, а значит a = 2. Обращаем внимание на то, что коэффициент при x³ равен 0
Выписываем в строчку a за ним коэффициенты многочлена
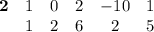
Под старшим коэффициентом пишем его же (в нашем случае 1), умножаем написанное на a (у нас 2) прибавляем к следующему коэффициенту (у нас 0). Результат записываем в следующую позицию второй строчки (1 · 2 + 0 = 2). С записанным числом повторяем те же действия (2 · 2 + 2 = 6), и так далее...
Получили частное x³ + 2x² + 6x + 2, остаток 5
Самая длиная линия из дорог A1, A2,___ Ak,
каждые два соседних города в этой последовательности соединены дорогой.
Если из городов A1 и Ak выходит ровно одна дорога .
Тогда пусть, например, из A1 идет дорога в город B, . Если B – один из городов A3, ___, Ak, то возникает цикл из дорог, что противоречит условию. Таким образом, город B отличвется от городов A1, A2, ___, Ak. Получается что в последовательности городов B, A1, A2, Ak города по парам размечены .
Соседние города соединены дорогой. Но эта последовательность содержит больше k городов не смотря на то что выбору последовательности A1, A2, Ak.
6/Задание № 1:
Сколько двузначных чисел, которые уменьшаются в 13 раз при отбрасывании последней цифры?
РЕШЕНИЕ: Пусть это число АВ=10a+b. При отбрасывании последней цифры возникает число A=a. Двузначное число в 13 раз больше однозначного, значит:
10a+b=13a
b=3a
Так как а и b цифры, то они должны быть целыми числами от 0 до 9, при чем а не совпадает с нулем, так как исходное число двухзначное.
Если а=1, то b=3 - число 13
Если а=2, то b=6 - число 26
Если а=3, то b=9 - число 39
Если а=4 и более, то b=12 и более - b не соответствует цифре
ОТВЕТ: 3 числа
6/Задание № 2:
Сколько чётных трёхзначных чисел, кратных 55, но не кратных 3?
РЕШЕНИЕ: Так как число, кратное 55, четно, то оно кратно 110. Таких чисел девять: 110, 220, 330, 440, 550, 660, 770, 880, 990. Очевидно, что три из них кратно 3, значит шесть - не кратно 3. Эти числа 110, 220, 440, 550, 770, 880.
ОТВЕТ: 6 чисел
6/Задание № 3:
Сумма двух чисел равна 764. Одно из чисел оканчивается пятёркой. Если эту пятёрку зачеркнуть, то получится второе число. Найдите разность этих двух чисел.
РЕШЕНИЕ: Пусть второе число х. Тогда первое выражается формулой 10х+5. Сумма этих чисел:
10х+5+х=764
11х=759
х=69
Разность этих чисел: 10х+5-х=9х+5=9*69+5=626
ОТВЕТ: 626