Даны точки P(-1,2,1); Q(3 ,-4 , 2) и плоскость 2x + 4y - 3z + 5=0.
Находим координаты вектора m, проходящего через точки P и Q.
m = (3-(-1)=4; -4-2=-6; 2-1=1) = (4; -6; 1).
Второй вектор - это нормальный вектор заданной плоскости. Он будет лежать в искомой плоскости. Его координаты берём из уравнения:
n = (2; 4; -3).
Теперь берём точку P(-1,2,1) и 2 вектора, которые будут лежать в искомой плоскости: m = (4; -6; 1) и n = (2; 4; -3).
Плоскость, проходящая через точку М0(х0;у0;z0) и параллельная данным (непараллельным между собой) прямым K1 и K2 (или векторам a1 и а2), представляется уравнением:
x-x0 y-y0 z-z0
nx ny nz
mx my mz = 0.
Подставляем данные:
x+1 y-2 z-1
2 4 -3
4 -6 1 = 0.
Решив эту матрицу, получаем -14x - 14y - 14z + 42 = 0.
Сократив на -14, получаем уравнение искомой плоскости:
x + y + z - 3 = 0.
1. Пусть было х трехместных и у пятиместных лодок.
x+y = 7
В трехместные лодки поместилось 3x чел, а в пятиместные 5y чел. Всего в лодках был 31 турист.
3x+5y = 31
Составим и решим систему уравнений:
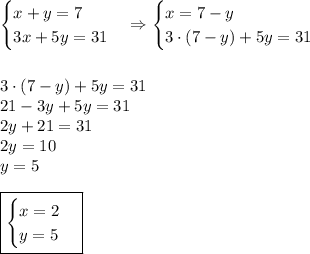 .
.
ответ: было 2 пятиместных и 5 трёхместных лодок.
2. Собственная скорость катера x км/ч, скорость течения реки y км/ч.
x+y км/ч скорость катера по течению
x-y км/ч скорость катера против течения
По течению 84 км проплыл за 3 часа:
(x+y)·3 = 84
Против течения 84 км проплыл за 3,5 часа:
(x-y)·3.5 = 84
Составим и решим систему уравнений:
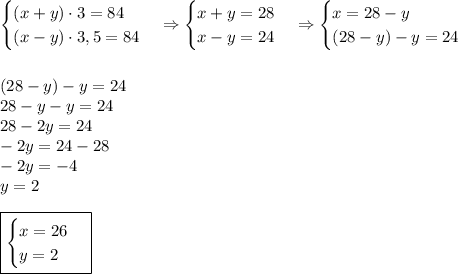
ответ: собственная скорость катера 26 км/ч, скорость течения реки 2км/ч.