Відповідь:
На окружности будет 8 точек.
Покрокове пояснення:
За какое-то время первый муравей пробегает 10 кругов, а второй за это же время пробегает 6 кругов. Соотношение скоростей муравьев 10 / 6. Значит за то время пока первый муравей пробежит 10 градусов круга, второй пробежит только 6 градусов. Примем за Х количество сегментов по 10° для первого муравья и по 6° для второго муравья, которые необходимы для того, что-бы они встретились.
10 × Х / 360 + 6 × Х / 360 = 1
16 × Х = 360
Х = 360 / 16 = 22,5°
22,5 × 10 = 225° - пробегает первый муравей до встречи.
22,5 × 6 = 135° - пробегает второй муравей до встречи.
Если бы оба муравья бежали бы с одинаковой скоростью, то они бы встретились на углу 180°.
Значит первый муравей спешит на
225 - 180 = 45°
а второй муравей отстает на
180 - 135 = 45°
Значит необходимо
360 /45 = 8 - встреч муравьев прежде, чем они снова вдвоем встретятся на угле 0°.
Проверка.
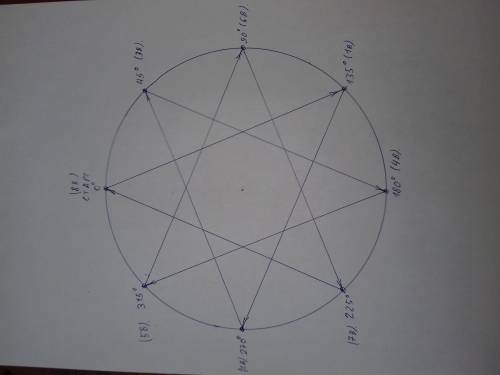
Старт - 0°
1 встреча - 135°
2 встреча - 270°
3 встреча - 45°
4 встреча - 180°
5 встреча - 315°
6 встреча - 90°
7 встреча - 225°
8 встреча - 0°
а)
∠ABC=180°-∠DAB=106°
∠BCD=∠ABC=106°
∠ADC=∠DAB=74°
ответ: ∠ADC=74°; ∠ABC=106°; ∠BCD=106°;
б)
∠EFG+∠HEF=180°
6x=180°
x=30°
∠EFG=2x+8°=68°
∠HEF=4x-8°=112°
∠FGH=∠EFG=68°
∠GHE=∠HEF=112°
ответ: ∠EFG=68°; ∠FGH=68°; ∠HEF=112°; ∠GHE=112°
Пошаговое объяснение:
По свойству трапеции сумма углов при боковой стороне равна 180°. Это следует из того, что основания трапеции по определению параллельны, а односторонние углы при секущей и параллельных прямых равны.
По свойству равнобокой(равнобедренной) трапеции углы при оснований равны.
переводим км в м
15000:30=500 м
2. Вычислим, сколько вторая бригада асфальтирует за один день
15000:60=250 м
3. Узнаем, сколько обе бригады асфальтируютза один день
500+250=750 м
4. Наконец, вычислм, за сколько дней обе бригады заасфальтируют дорогу, работая вместе:
15000:750=20 дней