2 л *6 банок=12 л
ответ: 12 литров.
Дана прямая как линия пересечения двух плоскостей:
{2x+y+z-2=0
{2x-y-3z+6=0.
Находим уравнение направляющего вектора этой прямой как векторное произведение нормальных векторов заданных плоскостей.
Это n1 = (2; 1; 1) и n2 = (2; -1; -3).
Векторное произведение векторов
a × b = {aybz - azby; azbx - axbz; axby - aybx}.
Подставим координаты векторов и получаем:
n1* n2 = X Y Z
-2 8 -4 .
Найдем какую-либо точку прямой . Пусть z = 0, тогда
2x + y = 2
2x - y = -6
4x = -4 x = -4/4 = -1.
y =2 - 2x = 2 - (2*(-1)) = 2 + 2 = 4.
Следовательно, (-1; 4; 0) – координаты точки, принадлежащей прямой.
Канонические уравнения прямой:
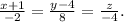
Автобус должен был забрать туристов в 17.00 и привезти на базу.
Пусть автобус должен был ехать t часов.
Значит время прибытия на базу (17.00+t) часов
На самом деле автобус прибыл на базу в (17.00+t) часов-20 минут=
(17.00+t-(1/3)) часов.
Чтобы прибыть на станцию к 17.00 автобус должен был выехать на t часов раньше, чем 17 часов.
Т.е автобус выехал в (17.00-t) , а приехал на базу в (17.00+t-1/3)
Автобус был в пути
(17.00+t-1/3)-(17.00-t)=2t-1/3
Причем до встречи и после встречи он проехал один и тот же путь c одной и той же скоростью.
Значит, до встречи с туристами автобус ехал (t-1/6) часа и встретив туристов ехал (t-1/6) часа
Туристы начали свое движение в 15.10 и прибыли на турбазу в (17.00+t-1/3)
Значит, туристы были в пути
(17.00+t-1/3)-15.10= 1час 50 мин +t -1/3 часа=1 час 30 мин +t
За это время они ехали на автобусе (t-1/6) часа
и
1час 30 мин +t - (t-1/6)=1 час 30 мин + 10 мин = 1 час 40 мин туристы шли пешком
Автобус должен был проехать путь 60t км до станции и 60t км после.
Всего 120 t
Фактически автобус проехал 60·2(t-1/6)=120t-20
Значит автобус проехал на 20 км меньше
Т.е он не доехал до станции половину этого расстояния, т.е 10 км
10 км туристы за 1 час 40 мин
10 км:1 целую 4/6 часа=10:(10/6)=6 км в час скорость туристов
6×2=12
На 6 2литровых банок нужно 12литр воды