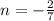 - знаменатель обращается в 0.
- знаменатель обращается в 0.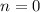 - по обычаю проверяется эта точка.
- по обычаю проверяется эта точка. (при
(при  →∞)
→∞)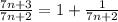

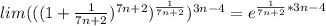 (при
(при  →∞)
→∞)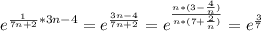 (при
(при  →∞)
→∞) →+∞ предел равен
→+∞ предел равен 
 →-∞ предел равен
→-∞ предел равен 
 →0 предел равен:
→0 предел равен:
 →
→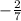
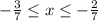 - мы получаем отрицательное основание).
- мы получаем отрицательное основание).
1. Часть речи
Часть речи слова укрыли -- глагол.
2. Морфологические признаки
Начальная форма: укрыть (инфинитив);
Постоянные признаки: 1-е спряжение, переходный, совершенный вид;
Непостоянные признаки: изъявительное наклонение, множественное число время.
3. Синтаксическая роль
Может быть различным членом предложения, смотрите по контексту.
1. Часть речи
Часть речи слова молочным -- имя прилагательное.
2. Морфологические признаки
Начальная форма: молочный (именительный падеж единственного числа мужского рода);
Постоянные признаки: качественное;
Непостоянные признаки: единственное число, творительный падеж, мужской род, полная форма.
3. Синтаксическая роль
Может быть различным членом предложения, смотрите по контексту.
1. Часть речи
Часть речи слова ночь -- имя существительное.
2. Морфологические признаки
Начальная форма: ночь (именительный падеж единственного числа);
Постоянные признаки: нарицательное, неодушевлённое, женский род, 3-е склонение;
Непостоянные признаки: именительный падеж, единственное число.
3. Синтаксическая роль
Может быть различным членом предложения, смотрите по контексту.
Пошаговое объяснение:
1)
дроби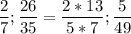 несократимые, поскольку числитель и знаменатель этих дробей - взаимно простые числа , то есть имеют единственный общий положительный делитель, равный единице.
несократимые, поскольку числитель и знаменатель этих дробей - взаимно простые числа , то есть имеют единственный общий положительный делитель, равный единице.
дробь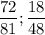 можно сократить
можно сократить
Получаем дроби :
Найдем общий знаменатель для этих дробей , для этого найдем НОК ( 7;8;9;35;49)
Разложим числа на простые множители. Сначала запишем разложение на множители наибольшего число, затем остальные числа.
49= 7*7
35 = 5 *7
7 = 7
8 = 2 *2* 2
9 = 3 *3
Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их:
НОК (7; 8; 9; 35) = 7* 7*5* 2 * 2 * 2 * 3 * 3 = 17640
Общий знаменатель будет 17640 , значит получим ряд дробей :
В ряду дробей с одинаковым знаменателем большей будет та у которой числитель больший . Упорядочим наш ряд :
Значит первоначальный ряд в порядке возрастания будет :
2) Решаем по тому же алгоритму
Несократимые дроби :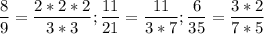
Сократимые :
Получили ряд дробей :
Найдем общий знаменатель , а для этого найдем
НОК ( 3;4;9;21;35)
35 = 5*7
21= 3*7
9= 3*3
4= 2*2
3= 3*1
НОК ( 3;4;9;21;35) = 5*7*3*3*2*2= 1260 - это и будет общий знаменатель
Упорядочим ряд по возрастанию :
Соответственно , первоначальный ряд в порядке возрастания будет