16÷65=16/65 ч первый а/м достигнет перекрестка.
(16/65)*45=11 1/13 км проедет второй а/м, когда первый достигнет перекрёстка.
12-11 1/3=12/13 км будет расстояние между первым а/м и вторым а/м.
Дальше смотрите рисунок к задаче, на рисунке перекрёсток. По началу я думал, что самая короткая гипотенуза между автомобилями будет тогда, когда расстояния от перекрёстка до первого и второго автомобиля будут равны. Оно бы так и было, если бы скорости у первого и второго автомобиля были бы равные.
В данном случае расстояние между автомобилями будет меняться по гипотенузе прямоугольного треугольника, когда первый автомобиль удаляется от перекрестка, а второй приближаться к перекрёстку (находясь от него на расстоянии 12/13 км.) Если записать функцию как квадрат гипотенузы, то:
f(t)=(0-65t)²+(12/13-45t)²=4225t²+(144/169)-(1080t/13)+2025t²=
=6250t²-(1080t/13)+(144/169)
Найдем наименьшее значение функции:
(1080/13)/(2*6250)=54/8125 часа после движения первого автомобиля от перекрёстка расстояние между автомобилями будет наименьшим.
16/65+54/8125=0,2528 часа=15,168 минут после начала движения, расстояние между автомобилями будет наименьшим.
(54/8125)*65=54/125 км проехал первый автомобиль от перекрёстка за 54/8125 часа.
(12/13)-(54/8125)*45=(12/13)-(486/1625)=78/125 км расстояние до перекрестка второго автомобиля, когда первый автомобиль отъехал от перекрестка на 54/125 км.
Найдём наименьшее расстояние между автомобилями по теореме Пифагора.
S=√(54/125)²+(78/125)²≈0,758946638≈0,76 км. наименьшее расстояние между автомобилями.
ответ: через 15,168 минут после начала движения, расстояние между автомобилями будет наименьшим: ≈ 0,76 км.
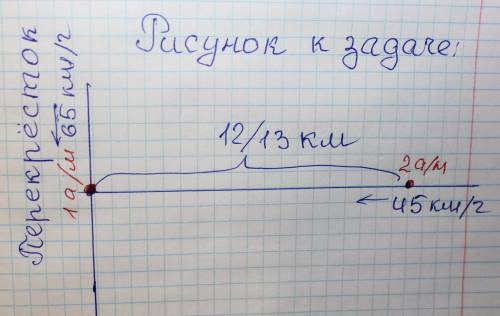
В начальный момент времени расстояние между машинами по теореме Пифагора
S0 = √(16^2 + 12^2) = √(256 + 144) = √400 = 20 км.
Расстояние от 1 машины до перекрестка меняется по закону:
s1 = 16 - 65*t км, где t - время в часах.
Расстояние от 2 машины до перекрестка меняется по закону:
s2 = 12 - 45*t км.
Расстояние между машинами по той же теореме Пифагора
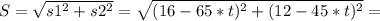
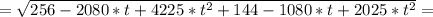
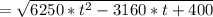
Вычислим минимум этой функции, который будет в вершине параболы
t0 = -b/(2a) = 3160/(2*6250) = 158/625 часов = 158*60/625 = 15,168 минут.
В этот момент машины проехали
s1 = 16 - 65*t0 = (16*625 - 65*158)/625 = -270/625 = -54/125
s2 = 12 - 45*t0 = (12*625 - 45*158)/625 = 390/625 = 78/125
То, что s1 < 0 говорит о том, что 1 машина уже проехала перекресток.
Расстояние между машинами в этот момент
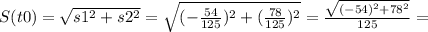
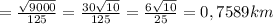
1) 18 и 36
2) 12 и 24
3) 6 и 12
4) 45 и 135