Найдем количество благоприятных нам исходов. Первый человек может родиться в любой из 12 месяцев. Чтобы дни рождения всех четырех людей приходились на разные месяца, второй должен родиться в любой из 11 оставшихся месяцев, третий - в любой из 10, и четвертый - в любой из 9. Таким образом, есть 12 · 11 · 10 · 9 благоприятных исходов.
Несложно убедиться, что всего исходов 12⁴ (так как день рождения у каждого может быть в любой из 12 месяцев).
Считаем искомую вероятность как отношение благоприятных исходов ко всем возможным исходам: 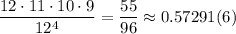
ответ: 55/96
Рассмотрим немного другую задачу. Выбрасываются k (k>0) кубиков, человек загадывает число от 1 до 6. Найти вероятность того, что число присутствует хотя бы на одном из кубиков
Событие А="число присутствует хотя бы на одном из кубиков" противоположно событию В="число не присутствует ни на одном из кубиков". Тогда 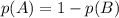
Вероятность не угадать число на одном кубике равна  (среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна
(среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна 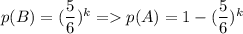 - это и есть искомая вероятность в данной задаче.
- это и есть искомая вероятность в данной задаче.
Вернемся к исходной задаче. На 1ом этапе вероятность угадать число равна 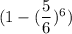 . При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна
. При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна 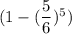 . При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна
. При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна 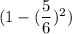
Тогда искомая вероятность 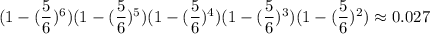
40
Пошаговое объяснение:
36:0,6=60 (км/ч) первая часть пути
100-60=40 (км/ч) разница