Квадрат - это четырехугольник, у которого все стороны равны, все углы равны (все углы прямые).
1) Зная периметр квадрата, найдем его сторону (a):
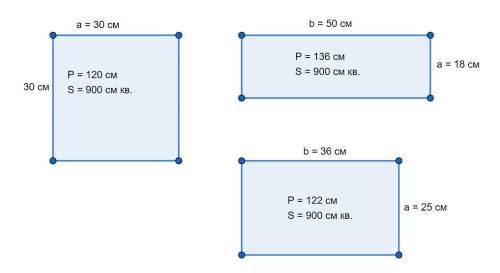
P(кв) = 4a = 120 см. a = 120/4 = 30 см.
Найдем площадь квадрата со стороной 30 см.
S кв = a*a = 30 см *30 см = 900 см кв.
2) Площадь прямоугольника равна произведению длины (a) на ширину (b).
S пр = a * b = 900 см кв.
а) Это может быть прямоугольник со сторонами 18 см и 50 см.
Его площадь равна площади заданного квадрата:
S₁ = 18 см * 50 см = 900 см кв.
Найдем периметр этого прямоугольника
P₁ = 2(a+b)=2(18 см + 50 см) = 2 * 68 см = 136 см.
Периметр квадрата меньше периметра прямоугольника. P < P₁
б) Прямоугольник со сторонами 25 см и 36 см. Его площадь также равна площади квадрата:
S₂ = 25 см * 36 см = 900 см кв.
Найдем периметр второго прямоугольника:
P₂ = 2(a+b)=2(25 см +36 см) = 2 * 61 см = 122 см.
Периметр квадрата меньше периметра прямоугольника. P < P₂.
Вывод. Периметр квадрата меньше периметра прямоугольника той же площади.
1) Для n=1 1/1*3 = 1/(2+1) - условие выполняется.
2) Пусть условие выполняется для n первых членов ряда, тогда, Для (n+1)-го слагаемого имеем значение
1/(2(n+1)-1)(2(n+1)+1) = 1/(2n-1)(2n+3) = 1/(4n^2+2n-3)
Найдём сумму первых (n+1) членов ряда:
n/(2n+1) + 1/(2n-1)(2n+3) = (n(4n^2+2n-3) + 2n + 1)/(2n+1)(2n-1)(2n+3) = (4n^3+2n^2-n+1)/(8n^3+12n^2-2n-3) = (n+1)(4n^2-2n+1)/(2n+3)(4n^2-2n+1) = (n+1)/(2n+3) = (n+1)/(2(n+1)+1) - Второе условие тоже выполняется, значит утверждение верно
Пошаговое объяснение: