1. √(12×3)=6
2. 4√3 - 3√3 -√3 = 0
3. 9x²-4=0
x=±√(4/9)=±2/3
ответ: -2/3;2/3.
4. D=b²-4ac, где а - коэффициент перед х², b - коэффициент перед х, с - коэффициент без х
D=25-4×2×3=1
5.
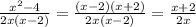
х≠2
При х=4(нужно просто подставить в формулу вместо х 4): 6/8=3/4
6. x1+x2=-b
x1x2=c, где b - коэффициент перед х, с - коэффициент без х
х1+х2=-7
7. х²-2х-3=0
х1+х2=2
х1х2=-3
ответ: -1;3.
8.
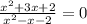
Корни первого уравнения: -2; -1, значит его можна записать как (х+2)(х+1)
Корни второго уравнения: -1; 2, значит его можна записать как (х+1)(х-2)

х≠-1; 2
х=-2
ответ: -2.
Если будут вопросы – обращайтесь :) Отметьте как лучший ответ, если не сложно ❤️
Если так не видишь,что эти уравнения похожи на обычные квадратные, то сделай замену х^2=t
а) х^4-3х^2+2=0 сделаем замену и получим:
t^2-3t+2=0, дальше по теореме Виетта ищем корни, которые видны сразу:
t=2
t=1 , дальше возвращаемся к изначальным переменным:
х^2=2
х^2=1, отсюда:
х=корень из 2
х=минус корень из 2
х=1
х=-1
Я думаю ты поняла и поэтому я опустила моменты с заменами. Если непонятно спрашивай
б)х^4-10х^2+9=0
х^2=9
х^2=1
ответ:х=3
х=-3
х=1
х=-1
в)х^4-5х^2+4=0
х^2=4
х^2=1
ответ:х=2
х=-2
х=-1
х=1
г)х^4-26х^2+25=0
х^2=25
х^2=1
ответ:х=5
х=-5
х=1
х=-1
д)х^4-20х^2+64=0
х^2=16
х^2=4
ОТвет:х=4
х=-4
х=2
х=-2
Допустим, берём (да, случайная выборка) 2 ученика, которые играют в волейбол, 3 ученика, играющие в баскетбол, 4 ученика, которые занимаются плаванием, 4 ученика, занимающиеся лёгкой атлетикой, также 4 ученика, играющие в теннис, 5 учеников, играющие в футбол, 6 учеников, занимающиеся гимнастикой, и 7 учеников, занимающиеся борьбой.
Из этого всего мы получаем таблицу ниже:
Волейбол - 2
Баскетбол - 3
Плавание - 4
Лёгкая атлетика - 4
Теннис - 4
Футбол - 5
Гимнастика - 6
Борьба - 7
Дальше, по заданию надо составить вариационный ряд.
Просто по возрастанию (уже сделано).
Дальше записать наименьшее и наибольшее значение варианты.
Наименьшее значение - 2;
Наибольшее значение - 7.
Объяснение:
Почему мы берём именно такое количество учеников?
Из-за того, что у нас случайная выборка, и ещё, надо ввести пример выборки из генеральной совокупности количества учащихся 7 и 8 классов, что означает, мы можем ввести любое (конечно в пределах нормы) значение.