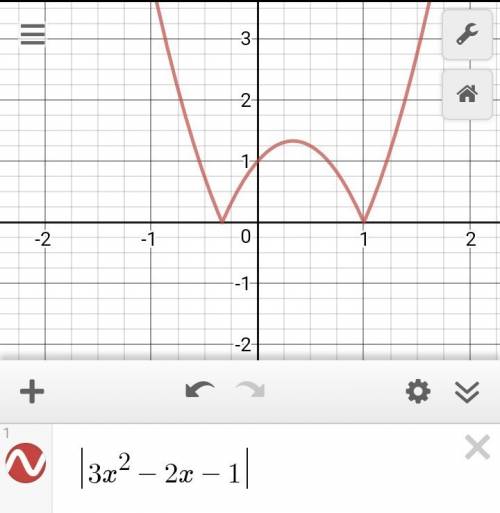
Сначала построим график функции, которая под модулем. Что делает модуль? Он все отрицательные ЗНАЧЕНИЯ делает положительными, то есть получив график функции нам надо будет всё что ниже оси Ох поднять наверх (отразить относительно оси Ох).
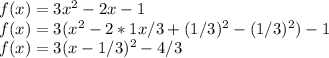
И так надо построить этот график. Это парабола, ветви которой вверх, координаты вершины (1/3;-4/3). И найдём точки пересечения с осями координат: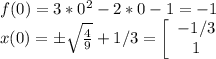 
Можем строить.
И так надо отразить относительно оси Ох значения функции f(x) на интервале от -1/3 до 1. Получилась нужная нам функция, её можно записать как:
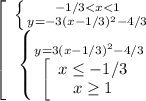
И естественно так как мы отразили относительно оси Ох, то значения вершины и точка пересечения с осью Оу.
Обозначим скорость скорого поезда за ν₁, а скорость товарного ν₂.
Тогда ν₂=ν₁-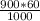
=ν₁-54 (км/ч)
(Умножение на 60 переводит минуты в часы, деление на 1000 переводит метры в километры)
Тогда получаем уравнение:
180/ν₂ - 180/ν₁ = 3
180/(ν₁-54) - 180/ν₁ = 3
180·ν₁-180·(ν₁-54) = 3·ν₁·(ν₁-54)
9720=3·ν₁²-162ν₁
3·ν₁²-162ν₁-9720=0
ν₁²-54ν₁-3240=0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-54)2 - 4·1·(-3240) = 2916 + 12960 = 15876
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 54 - √158762·1 = 54 - 1262 = -722 = -36
x2 = 54 + √158762·1 = 54 + 1262 = 1802 = 90
Так как скорость у нас положительная (поезд движется вперед), то выбираем х₂=ν₁=90 км/ч - скорость скорого поезда.
Тогда скорость товарного поезда:
ν₂=ν₁-54=90-54=36 км/ч
ответ: 36 км/ч
Проверка: 180/36 - 180/90 = 5-2=3. Все верно.