Найдём уравнение касательных к графику функции f(x) = -8x-x².
f'(x) = -(8x)'-(x²)' = -8-2x
Уравнение для касательной с абсциссой точки касания x₁ = -6:
f'(x₁) = f'(-6) = -8-2·(-6) = -8+12 = 4;
f(x₁) = f(-6) = -8·(-6)-(-6)² = 48-36 = 12;
y = f'(x₁)·(x-x₁)+f(x₁) = 4·(x-(-6))+12 = 4x+24+12 = 4x+36.
Уравнение для касательной с абсциссой точки касания x₂ = 1:
f'(x₂) = f'(1) = -8-2·1 = -8-2 = -10;
f(x₂) = f(1) = -8·1-1² = -8-1 = -9;
y = f'(x₂)·(x-x₂)+f(x₂) = -10·(x-1)+(-9) = -10x+10-9 = -10x+1.
Стороны треугольника лежат на прямых:
y = 4x+36; y = -10x+1; x = 0.
Найдём вершины треугольника.
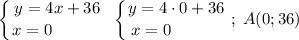
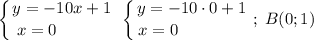
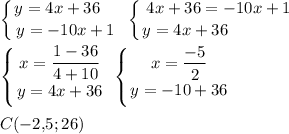
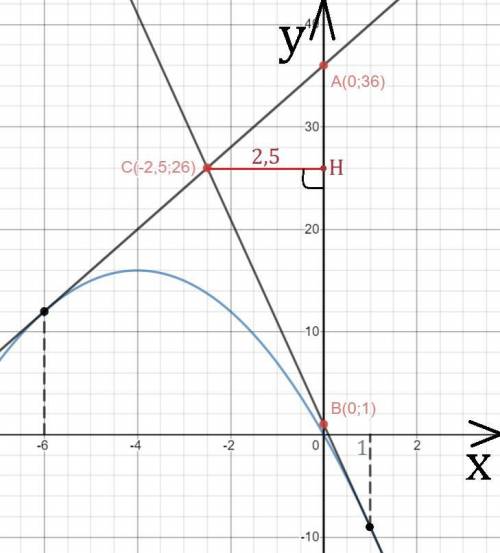
Сторона AB лежит на оси Oy, поэтому высота CH, треугольника ABC, будет параллельна оси Ox. А значит, CH = |-2,5| = 2,5.
AB = 36-1 = 35, поскольку эта сторона перпендикулярна оси Ох.
Площадь треугольника равна полупроизведению его высоты и стороны к которой она проведена.
S(ABC) =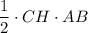 
= 2,5·35/2 = 175/4 = 43,75
ответ: 43,75.
Відповідь:
y=1-2x
5x+2y=0 - в это уравнение нужно вместо y подставить 1-2x
5x+2(1-2x)=0 - ну и открываем скобки и считаем чему равен x
5x+2-4x=0
x=-2 - теперь возвращаемся к уравнению y=1-2x (вместо x подставляем -2)
y=1-2*(-2)
y=5
ответ (-2;5) - на первое место ставим значение икса
второе методом подстановки решить не получиться... только так
3x+2y=8 *(-3)
2x+6y=10
-9x-6y=-24
2x+6y=10
-9x-6y+2x+6y=-24+10
(-6y и6y сокращаются )
-9x+2x=-14
-7x=-14
x=2
подставляем X в уравнение
3*2+2y=8
6+2y=8
2y=8-6
2y=2
y=1
(2;1)
2(к-х)-расстояние, которое лодка, плывущая против течения реки.
Составим и решим уравнение:
2(к+х)-2(к-х)=16
2к+2х-2к+2х=16
4х=16
х=4
ответ:4 км/ч скорость течения реки.