Дана функция
f(x)=4+3·x-x²
1) координаты точек пересечения графика с осью абсцисс:
f(x)=0 ⇔ 4+3·x-x²=0 ⇔ x²-3·x-4=0: D=(-3)²-4·1·(-4)=9+16=25=5²
x₁=(3-5)/(2·1)= -2/2= -1; x₂=(3+5)/(2·1)= 8/2= 4.
ответ: (-1; 0), (4; 0).
2) координаты точек пересечения графика с осью ординат:
f(0)=4+3·0-0²=4
ответ: (0; 4).
3) координаты точек пересечения графика с прямой y=-2·x²+3:
f(x)=y ⇔ 4+3·x-x²=-2·x²+3 ⇔ x²+3·x+1=0 : D=3²-4·1·1=9-4=5
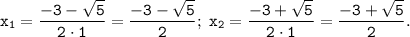
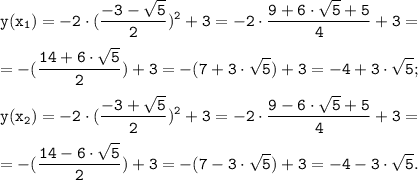
ответ: 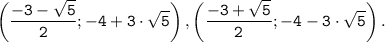
4) наибольшее значение функции:
f(x)=4+3·x-x²=-(x²-3·x-4)=-(x²-2·(3/2)·x+(3/2)²-(3/2)²-4)=
=-(x²-2·(3/2)·x+(3/2)²)+(3/2)²+4=4+9/4-(x-3/2)²=6,25-(x-1,5)²≤ 6,25
Отсюда, если (x-1,5)²=0, то получаем наибольшее значение функции.
ответ: 6,25.
![1/ \sqrt[4]{2}](/tpl/images/0631/9349/a5b12.png)
![\sqrt[4]{ \sqrt{10}- \sqrt{2} }](/tpl/images/0631/9349/98dda.png)
(3а-5)\(а-1)<1 а≠1
3а-5<а-1
3а-а<-1+5
2а<4
а<1
0- Не натуральное число, 1 исключается, т.к знаменатель равен 0, значит, такого натурального числа нет. (ответ не мой)