Задание № 5:
Стоя неподвижно на ступени эскалатора в метро Ваня поднимается наверх за одну минуту. Взбегая по ступеням неподвижного эскалатора, он добирается до верха за 40 секунд. За какое время Ваня поднимается наверх, если начинает взбегать по ступеням эскалатора, движущегося вниз? Дайте ответ в секундах.
РЕШЕНИЕ: Пусть длина расстояния L.
Если Ваня взбегает по ступеням неподвижного эскалатора, то скорость движения равна L/40. (Считаем в секундах, в минуте 60 секунд).
Если Ваня стоит неподвижно на ступени эскалатора, то скорость движения равна L/60.
Когда Ваня бежит по ступеням движущегося вниз эскалатора, то скорости Вани и эскалатора вычитаются: L/40-L/60. Тогда время определяется отношением длины к скорости:
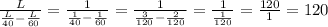
ОТВЕТ: 120 секунд
Задание № 1:
Найдите последнюю ненулевую цифру значения произведения 40^50*50^40?
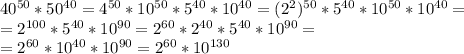
10^130 нас не интересует. Попробуем повозводить 2 в степень:
2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32
Пятая степень, как и первая, оканчивается на 2. Образуется своего рода цикл.
Чтобы узнать последнюю цифру степени N, нужно N разделить на 4. Остаток от деления соответствует степени, последняя цифра которой совпадает с последней цифрой степени N. Остаток 0 соответствует 4-ой степени.
60/4=15, остаток 0 – 4 степень оканчивается на 6, значит и 60 степень оканчивается на 6
ОТВЕТ: 6
Задание № 3:
Сколько корней имеет уравнение: |x|=|x−1|+x−3?
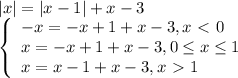
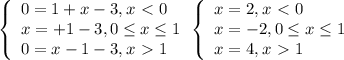
Условию раскрытия модуля соответствует только третья строчка.
ОТВЕТ: 1
(50; 250)
(-0,9; 9,95)
Объяснение:
Пусть функция задана формулой у = ах² + bx + c/
Абсциссу вершины параболы находить можно по формула х = -b/(2a), а ординату, подставив найденное значение абсциссы в формулу.
1) y = −0,1x² + 10x
х вершины = - 10/(2·(-0,1)) = - 10/(-0,2) = 100/2 = 50;
у вершины = у(50) = − 0,1·50² + 10·50 = − 0,1·2500 + 500 = - 250 + 500 = 250.
(50; 250) - вершина параболы.
2) y = 5x² + 9x + 14
х вершины = -9/(2·5) = - 0,9;
у вершины = у(- 0,9) = 5·(-0,9)² + 9·(-0,9) + 14 = 5·0,81 - 8,1 + 14 = 4,05 - 8,1 + 14 = 9,95.
(-0,9; 9,95)