Вариант 2
Часть 1
А1. У выражение:
a6 2) a10 3) a2
А2. Одна сторона прямоугольника равна a, вторая 3. Найдите периметр прямоугольника.
1) Р = 2(а + 3) 2) Р = а + 6 3) Р = 2а + 3 4) Р = 4 (а + 3)
А3. У выражение: 12а4 b8: (- 6а4b4)
1) – 2аb2 2) – 2b2 3) 2b4 4) – 2b4
А4. У х2 у . (-3)х3 у
1) 6x5y2 2) 6x6y 3) – 6x5y2 4) – 6x6y
А5. У выражение (а – 5)(а +3) +2а + 15 и найдите его значение при а = – 1
1) 1 2) – 1 3) 16 4) 2
Часть 2
В1. К многочленам подберите соответствующий им разложения на множители
1) 25х2 +16у2 2) 8ху2 + 4х2 3) а3 – b3 4) 3а2 +3аb –а – b
А) вынесение общего множителя за скобки
Б) формула сокращенного умножения
В) не раскладывается на множители
Г группировки
1
2
3
4
В2. Постройте график функции у= – 3х +4
Часть 3
С1. Решите уравнение: (3 – 2х)2 – (– 10х + 4 х2) = – 20.
С2. Решите систему уравнений:
через данную точку, мы должны, взять значение икса в данной точке, и подставить данное значение в функцию:
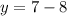
Заметим, что периметр шоколадки станет равным 10, если она будет состоять из прямоугольников 1 x 4 или 2 x 3, т. е. по одной стороне одна клетка, по другой 4 или по одной 2 клетки, по другой 3. По условию Петя начинает игру первый. Покажем, что у него существует выигрышная стратегия. Допустим, что после его очередного хода шоколадка приняла форму квадрата со сторонами 5 x 5. В этом случае, какой бы ход ни сделал Вася, Петя побеждает следующим ходом. Это наглядно показано на рисунке. Следовательно, Петина стратегия заключается в урезании шоколадки на каждом своем ходу до квадрата. На первом ходу он отламывает от шоколадки кусок 1 x 2019, превращая шоколадку в квадрат 2019 x 2019. Затем каждый раз, когда Вася отламывает n клеток по горизонтали, Петя отламывает n клеток по вертикали, превращая шоколадку в квадрат размером (2019-n) x (2019-n). В результате найдется Васин ход, после которого по горизонтали или по вертикали шоколадки останется не более пяти клеток. Следующим своим ходом Петя либо сразу побеждает, если клеток менее пяти, либо урезает шоколадку до квадрата размером 5 x 5, если клеток ровно 5. Далее после любого Васиного хода Петя побеждает
Объяснение:
шик ответ