Бісектриса гострого кута паралелограма ділить відрізки 6 і 8 см рахуючи від вершини тупого кута. знайти периметр. два прямокутники мають периметр по 122 см. основа 1-ого прямокут. більша за основу другого на 5 см. площа 2-ого прямокут.більша на 120^2. знайти площу кожного прямокутника
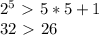 .
. 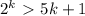 .
.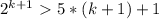
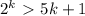 =>
=> 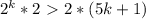 =>
=> 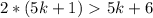
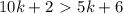 .
. 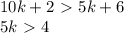
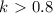 .
.
1)мы извлечем корень из левой и правой части в первом выражении,а вовтором домножим на 2 и получим
х+у=26
ху=120
2)теперь мы в первом выражении выразим у через х,а во второе выражение подставим значения
у=26-х
х*(26-х)=120
3)сейчас выносим второе ввыражение и решаем его
х(26-х)=120
26х-х^2-120=0 /домножим на (-1)(чтобы избавится от минуса при х^2)
х^2-26х+120=0
D= 676-480=196
х1= (26-14)/2=6
х2=(26+14)/2=15
4) подставим значения х в первое выражение во втором действии.
у=26-х=26-6=20 или у=26-х=26-15=11
ответ:(6;20) или(15;11)