Т.к отношение площадей треугольников равно квадрату коэффициента подобия, то к=3,а SАОD /SВОС=3^2, т.е 9.
Четыре числа образуют геометрическую прогрессию. Если к ним прибавить соответственно 6, 12, 14 и 8, тогда получим четыре числа, которые образуют арифметическую прогрессию. Найди числа, которые образуют геометрическую прогрессию.
знаменатель геометрической прогрессии: q= 2
члены геометрической прогрессии :
b1= 4
b2=8
b3= 16
b4=32
Решение
b₁; b₁·q; b₁·q²; b₁·q³ геометрическая прогрессия
тогда
b₁+6; b₁·q+12; b₁·q; b₁·q³ арифметическая прогрессия
по характеристическому свойству арифметической прогрессии
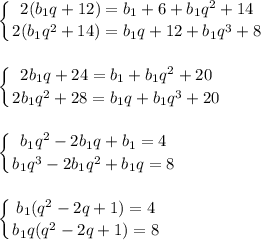
q ≠ 1
разделим второе уравнение на первое
q = 2
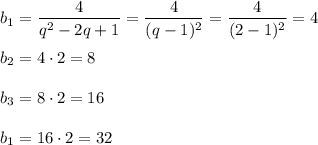
ж)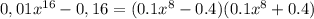
з)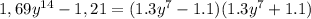
и) четыре девятых m в6-двадцать пять тридцать шестой = две третих m в 3 минус пять шестых умножить на две третих m в 3 плюс пять шестых