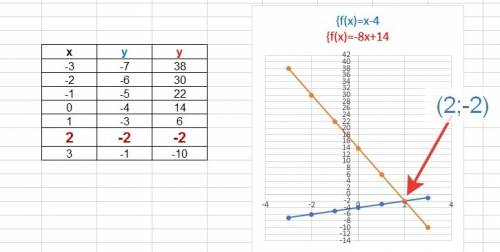
Пара чисел (2;-2) являются точкой пересечения двух графиков. заданных уравнениями системы.
Общее уравнение прямой: Ах+Ву+С=0
х=2; у=-2
1 уравнение: пусть А=4; В=-4, тогда 4х-4у+С=0
4*2-4*(-2)=16
С=0-16=-16
4х-4у-16=0
2 уравнение: пусть А=8; В=1, тогда: 8х+у+С=0
8*2+1*(-2)=14
С=0-14=14
8х+у-14=0
{4x-4y-16=0 => x-y-4=0 => x=y+4
{8x+y-14=0 => 8(y+4)+y-14=0
9y=-18
y=-2
x=-2+4
x=2
Решением данной системы является пара чисел (2;-2)
Проверка: 4x-4y-16=8x+y-14
4х-8х-4у-у-16+14=0
-4х-5у-2=0
х=2; у=-2 - -4*2-5*(-2)-2=
-8+10-2=
-10+10=0
Выразим у через х для графического решения:
{4x-4y-16=0 =>у=х-4
{8x+y-14=0 => у=-8х+14
График во вложении
p(x)=(2х+1)(4х^2-2х+1)-8х^3=(8х^3-4x^2+2x+4x^2-2x+1)-8x^3=1
То есть при любых значениях х ответ будет всегда 1.
23.18р(х;у)=(ху+3)(2ху-4)-2(ху-7)=2*x^2*y^2-4xy+6xy-12-2xy+14=2*x^2*y^2+2
Разберем по частям 2*x^2*y^2+2
1)
2*x^2*y^2 всегда положителен, так как квадрат числа не может быть отрицательным, положительное число{2}умножаем{x^2}и умножаем на {y^2} = положительное число, всегда положителен
2)
число 2>0, положительное число
3) сумма двух положительных чисел {2*x^2*y^2 и 2} всегда дает нам положительное число