Пусть . Переформулируем задачу, сведя ее к параметру: найдите максимальное значение параметра , при котором система имеет хотя бы одно решение. Первое уравнение задает прямую в , а второе — окружность с центром в начале координат радиусом 1. Заметим, что увеличивая , мы поднимаем прямую, значит, максимальному соответствует случай касания прямой и окружности.
. По теореме Пифагора найдем . При этом, очевидно: , подставляем: .
1) Разрешим наше дифференциальное уравнение относительно производной - уравнение с разделяющимися переменными Воспользуемся определением дифференциала Интегрируя обе части уравнения, получаем - общее решение
Разделяем переменные
интегрируя обе части уравнения, получаем
- общий интеграл
Решение задачи Коши нет, т.к. при х=0 логарифм ln0 не существует
Пример 3. Убедимся, является ли дифференциальное уравнение однородным.
Итак, дифференциальное уравнение является однородным. Исходное уравнение будет уравнением с разделяющимися переменными если сделаем замену , тогда
Подставляем в исходное уравнение
Получили уравнение с разделяющимися переменными
Воспользуемся определением дифференциала
Разделяем переменные
Интегрируя обе части уравнения, получаем
Обратная замена
- общий интеграл
Пример 4. Это дифференциальное уравнение второго порядка с постоянными коэффициентами также однородное. Воспользуемся методом Эйлера Пусть , тогда будем иметь характеристическое уравнение следующего вида:
Тогда общее решение будет иметь вид:
- общее решение Пример 5. Аналогично с примером 4) Пусть , тогда получаем
Пусть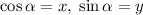 . Переформулируем задачу, сведя ее к параметру: найдите максимальное значение параметра
. Переформулируем задачу, сведя ее к параметру: найдите максимальное значение параметра  , при котором система
, при котором система 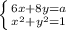 имеет хотя бы одно решение. Первое уравнение задает прямую
имеет хотя бы одно решение. Первое уравнение задает прямую 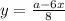 в
в 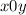 , а второе — окружность с центром в начале координат радиусом 1. Заметим, что увеличивая
, а второе — окружность с центром в начале координат радиусом 1. Заметим, что увеличивая  , мы поднимаем прямую, значит, максимальному
, мы поднимаем прямую, значит, максимальному  соответствует случай касания прямой и окружности.
соответствует случай касания прямой и окружности.
ответ: 10