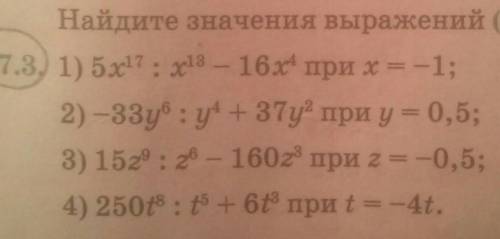
Пусть будет x коробок по 90 р и y коробок по 50 р.
Всего истратили 1300 р.
90x + 50y = 1300
9x + 5y = 130
Это так называемое диофантово уравнение, то есть с несколькими переменными. Его нужно решить в натуральных числах.
Применим такой прием.
y = (130 - 9x)/5 = 26 - (5x + 4x)/5 = 26 - x - 4x/5
Чтобы у было натуральным, х должно делиться на 5.
Решения: 1) x = 5, y = 26 - 5 - 4*1 = 17; Всего 5 + 17 = 22 коробки.
2) x = 10, y = 26 - 10 - 4*2 = 8; Всего 10 + 8 = 18 коробок.
Других вариантов нет.
ответ: наибольшее число коробок 22.
Найдем, чему равна скорость второго велосипедиста.
Согласно условию задачи, скорость первого велосипедиста равна с км/ч, а скорость второго велосипедиста на 3 км/ч больше, следовательно, скорость второго велосипедиста составляет с + 3 км/ч.
Найдем, чему равна скорость сближения велосипедистов.
Согласно условию задачи, велосипедисты едут навстречу друг другу, следовательно, скорость, с которой они сближаются составляет с + с + 3 = 2с + 3 км/ч.
Поскольку расстояние между пунктами А и В равно 35 км, то велосипедисты встретятся через 35/(2с + 3) часов.
ответ: велосипедисты встретятся через 35/(2с + 3) часов.
Объяснение:
Решение / ответ:
1) 5x¹⁷ ÷ x¹³ - 16x⁴ =
= 5x¹⁷⁻¹³ - 16x⁴ =
= 5x⁴ - 16x⁴ =
= - 11x⁴.
При x = - 1,
- 11x⁴ = - 11 × (- 1)⁴ = - 11 × 1 = - 11.
2) - 33y⁶ ÷ y⁴ + 37y² =
= - 33y⁶⁻⁴ + 37y² =
= - 33y² + 37y² =
= 4y².
При y = 0,5 ,
4y² = 4 × (0,5)² = 4 × 0,25 = 1.
3) 15z⁹ ÷ z⁶ - 160z³ =
= 15z⁹⁻⁶ - 160z³ =
= 15z³ - 160z³ =
= - 145z³.
При z = - 0,5 ,
- 145z³ = - 145 × (- 0,5)³ = - 145 × (- 0,125) =
= 18,125.
4) 250t⁸ ÷ t⁵ + 6t³ =
= 250t⁸⁻⁵ + 6t³ =
= 250t³ + 6t³ =
= 256t³.
При t = - 4t,
t = - 4t;
t + 4 t = 0;
5t = 0;
t = 0 ÷ 5;
t = 0.
256t³ = 256 × (0)³ = 256 × 0 =
= 0.
Удачи! :)