206. Найдите 5-й член арифметической прогрессии: 1) 19; 15; 11;...; 2) -1; 3; 7; ... .
-
207. Напишите первые четыре члена арифметической прогрессии {a}:
1) а, -10; d-4; 2) а, -1,7;d=-0,2; 3) а, -3,5; d-0,6; 4) а
6
208. Найдите: 1) а, если а, -3, d=0,7; 2) а если a, 18, d=-0,5;
3) а, если a, 20, d=3; 4) b, если b, 5,8, d=-1,5.
209. Найдите 5-й и пъй члены арифметической прогрессии: 1) -1;
...; 2) 2,3; 1; ...; 3) -8; -6,5; ...; 4) 11; 7; ... .
210. Даны первый член а и разность d арифметической прогрессии
{a ). Найдите а:
1) а, -2; d-0,1; n= 5; 2) а, -2,3; d=-1; n=10;
3) а, -3; d-0,8; п-16;
n61.
4) а1
211. Найдите разность d, если: 1) а, -2, ao-92; 2) а, -7, а 2;
3) а, -0, а-92.
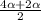sin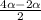
=2cos3α*sinα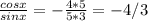
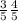=-24/25
х = 32, у = 29.
Объяснение:
Записываем условие:
x - y = 3
x^2 - y^2 = 183
Выражаем y через х из первого уравнения.
y = x - 3
Заменяем y во втором уравнении.
x^2 - (x - 3)^2 = 183
Раскрываем x - 3 по правилу сокращенного умножения
(a - b)^2 = a^2 - 2ab + b^2
(x - 3)^2 = x^2 - 6x + 9
Записываем все в одно уравнение:
x^2 - (x^2 - 6x + 9) = 183
Раскрываем скобки, меняя знаки.
x^2 - x^2 + 6x - 9 = 183
6x - 9 = 183
6x = 192
x = 192/6 = 32
Следовательно y = x - 3 = 32 - 3 = 29.
Проверяем:
32 - 29 = 3
32^2 = 1024; 29^2 = 841; 1024 - 841 = 183
Все верно.