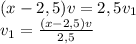
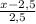раза выше. Приравняем теперь полное расстояние между пунктами А и В. Время в пути для велосипедиста Х, для мотоциклиста Х-12, скорость велосипедиста v, скорость мотоциклиста - 
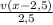, S=t*v.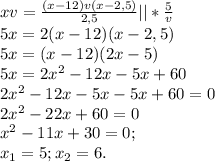
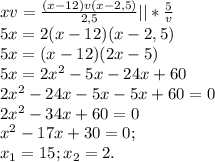
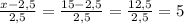раз выше скорости велосипедиста. Следовательно, на дорогу ему нужно впятеро меньше времени. 15/5=3, 15-12=3. ответ верен.
Вообще говоря, квадратное уравнение ВСЕГДА имеет 2 корня. Они могут быть:
1) разными действительными числами (если дискриминант уравнения положителен);
2) одинаковыми действительными числами (если дискриминант равен нулю);
3) комплексными сопряжёнными числами (если дискриминант отрицателен).
Но если, как это делается в школе, рассматривать только действительные корни, и при этом два равных корня считать одним, то при таких условиях уравнение будет иметь 2 корня только в случае, если дискриминант положителен.