a) x+y=12 _ x=12-y _ x=12-y
xy=32 (12-y)y=32 12y-y^2=32
y^2-12y+32=0
D=144-4*32=16
y1=(12+4)/2=8 x1=12-8=4
y2=(12-4)/2=4 x2=12-4=8
б) y=x+2 _ y=x+2 _ y=x+2
4y+x^2=8 4(x+2)+x^2=8 4x+8+x^2=8
x^2+4x=0
x(x+4)=0
x1=0 y1=2
x2=-4 y2=-4+2=-2
Не могу понять ,зачем решать графически ,когда эта интерпретация и есть аналитическое решение ,только в другой форме?
Причём в такой форме ,что не является обоснованным доказательством нашего корня или чего-нибудь другого
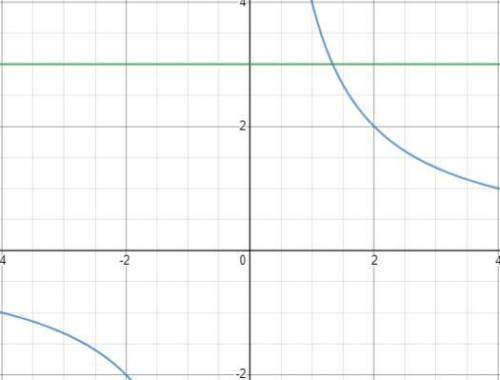
В первом ,да и как во втором уравнении ,у нас справа обратная пропорциональность
Первое уравнение!
Так как ,число а>0 в нашем случаи это 4 ,то функция располагается в первой и третьей четвертях
Так как у нас константа 3 ,то решение будет одно!
Так как просят решить графически ,то ссылаясь на один корень ,то он просто угадывается и это 4/3
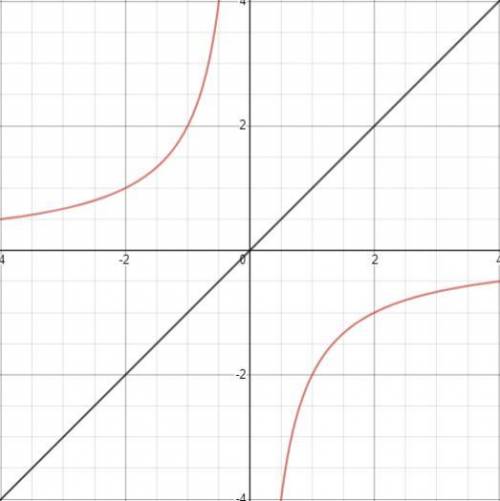
Второе уравнение!
Так как ,число a<0 в нашем случаи это -2,то функция будет располагаться во второй и четвёртой четвертях
Но как можно видеть,слева у нас f(x)=x - прямая
Данная прямая располагается в первой и четвёртых четвертях,так как a>0 ,следовательно данное уравнение не имеет решений!
a) x+y=12
xy=32
x=12-y
(12-y)y=32
12y-y²-32=0
y²-12y+32=0
y=4 x=8
y=8 x=4
б)y=x+2
4y+x²=8
4(x+2)+x²-8=0
4x+x²=0
x=-4 y=-2
x=0 y=2