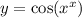
Мы видим, что данная функция является сложной, поэтому будем её дифференцировать как сложную.
Формула
d/dx( f(g(x)) ) = f'(g(x)) × g'(x), где в нашем случае f(x) = cos(x), а g(x) = x^x.
Для применения правила дифференцирования сложной функции, заменим x^x новой переменной t.
Дифференцируем
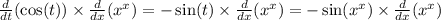
Для упрощения производной запишем х^х как e^( ln(x^x) ).
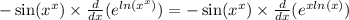
И опять сложная функция.
Дифференцируем её аналогично:
f(x) = e^x, g(x) = xln(x)
Заменим xln(x) перевенной k:
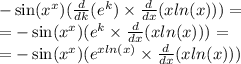
За правилом производной произведения имеем:
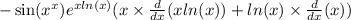
Вычисляем все производные и получаем:
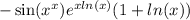
Это и есть ответ.
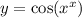
Мы видим, что данная функция является сложной, поэтому будем её дифференцировать как сложную.
Формула
d/dx( f(g(x)) ) = f'(g(x)) × g'(x), где в нашем случае f(x) = cos(x), а g(x) = x^x.
Для применения правила дифференцирования сложной функции, заменим x^x новой переменной t.
Дифференцируем
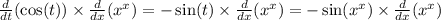
Для упрощения производной запишем х^х как e^( ln(x^x) ).
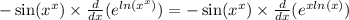
И опять сложная функция.
Дифференцируем её аналогично:
f(x) = e^x, g(x) = xln(x)
Заменим xln(x) перевенной k:
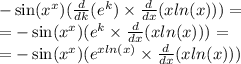
За правилом производной произведения имеем:
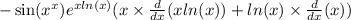
Вычисляем все производные и получаем:
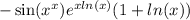
Это и есть ответ.
Формула функции выражает зависимость величин друг от друга, то есть изменение значения х по некой формуле f(x), влечет за собой изменение значения у.
х - переменная величина, может принимать любые значения;
у - величина, зависимая от изменения х.
Для аргумента х существует область определения D(y), при которой функция имеет смысл, то есть - у принимает какое-либо значение.
Для у существует область значений Е(у) - какие значения принимает у при допустимых значениях х.
Если, по условию, y>0 или y<0, то необходимо найти такие значения х. при которых данное неравенство выполняется.
Например: у=2x-2, или f(x)=2x-2, y>0, при x>1 - х∈(1;+∞),
y<0, при х<1 - x∈(-∞;1)
Значение х=1 в ОДЗ данных неравенств не входит,
т.к. при х=1, у=0
Во вложении график f(x)=2x-2 с таблицей значений