ответ: 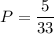 .
.
Трамваев = 5 , троллейбусов = 7 . Всего 5+7=12 машин.
Отъехало 4 машины.
Если среди 4-х машин отъехало не менее 3-х трамваев. Это значит, что отъехало либо 3, либо 4 трамвая. Выражение " не менее трёх" означает "больше либо равно трём".
Если отъехало 3 трамвая, то обязательно будет ещё 1 троллейбус, так как отъезжало 4 машины. А если отъехало 4 трамвая, то троллейбусы уже не будут отъезжать .
Вероятность того, что отъедет 3 трамвая и 1 троллейбус равна
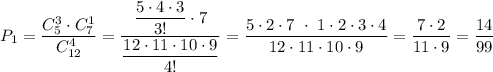
Вероятность того, что отъедет 4 трамвая равна
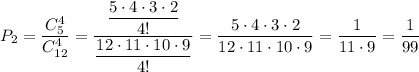
Вероятность того, что среди отъехавшего транспорта не менее трёх трамваев равна
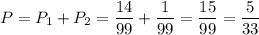
В решении.
Объяснение:
Решить уравнения:
1) х² - 10х - 24 = 0
D=b²-4ac = 100 + 96 = 196 √D=14;
х₁=(-b-√D)/2a
х₁=(10-14)/2
х₁= -4/2
х₁= -2;
х₂=(-b+√D)/2a
х₂=(10+14)/2
х₂=24/2
х₂=12;
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
2) 3х² - 7х + 4 = 0
D=b²-4ac = 49 - 48 = 1 √D=1;
х₁=(-b-√D)/2a
х₁=(7-1)/6
х₁= 6/6
х₁= 1;
х₂=(-b+√D)/2a
х₂=(7+1)/6
х₂=8/6
х₂=4/3;
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
3) 9у² + 6у + 1 = 0
D=b²-4ac = 36 - 36 = 0 √D=0;
у=(-b±√D)/2a
у=(-6±0)/18
у = -6/18
у = -1/3.
Проверка путём подстановки вычисленного значения у в уравнение показала, что данное решение удовлетворяет данному уравнению.
4) 3р² + 2р + 1 = 0
D=b²-4ac = 4 - 12 = -8
D < 0;
Уравнение не имеет действительных корней.
1) x<0,5 или x∈(-∞;0,5)
2)x∈∅
Объяснение:
8х+2<7-2x
перенесем х из одной части уравнения в другую с противоположным знаком
10x+2<7
теперь перенесем так же числа
10x<5
x<0,5
(x+1)(x-2)<x-3
раскроем скобки
x^2+x-2x-2<x-3
складываем подобные слагаемые
x^2-x-2<x-3
переносим переменные и числа с изменением знака
x^2-2x+1<0
применяем формулу сокр. умножения - квадрат разности
(x-1)^2<0
квадрат числа не может быть отрицательным⇒
x∈∅ (нет решений)