|x-1| + |x-a| = 1 - a
Сразу заметим, что левая часть ≥ 0, значит и правая часть должна будет тоже быть ≥ 0 :
1 - a ≥ 0
a ≤ 1
Теперь может найти подмодульные нули :
1) x - 1 = 0 2) x - a = 0
x = 1 x = a
Выставим их на числовой прямой и заметим, что а будет находиться сзади 1, так как мы выяснили что а ≤ 1, а при а = 1 есть только один корень :
x < a a ≤ x < 1 x ≥ 1
(a)(1)
Рассмотри три случая :
1) x < a
-x + 1 - x + a = 1 - a
-2x + 2a = 0
2(a - x) = 0
x = a - не подходит, т.к x < a
ответ : x ∈ ∅
2) a ≤ x < 1
-x + 1 + x - a = 1 - a
0 = 0
x ∈ R
ответ : x ∈ [a ; 1)
3) x ≥ 1
x - 1 + x - a = 1 - a
2x = 2
x = 1
ответ : x = 1
Соединим все наши решения :
[ x ∈ ∅
[ x ∈ [a ; 1)
[ x = 1
x ∈ [a ; 1]
Уравнение будет иметь ровно 3 целых решения, если а = -1.
Уравнение будет иметь 3 и больше решений при а ≤ -1
Раскрываем знак модуля:
Если cosx >0, то |cosx|=cosx
уравнение принимает вид:
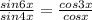
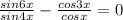
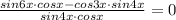
По формуле произведения синуса на косинус:
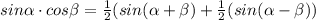
тогда
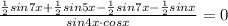
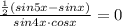
По формуле разности синусов:
⇒ 
⇒ 
⇒ 
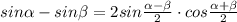
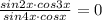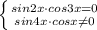
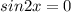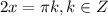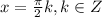
или
⇒ 
⇒ 
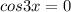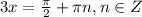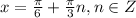
и
⇒ 
⇒ 
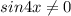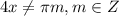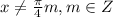
и
⇒ 
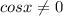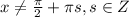
О т в е т первого случая c учетом cosx >0:
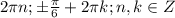( см. рис.1)
Если cosx <0, то |cosx|= - cosx
уравнение принимает вид:
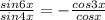
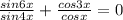
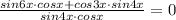
По формуле синуса двойного угла
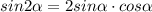
тогда
⇒ 
⇒ 
⇒ 
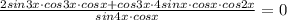
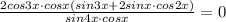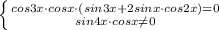
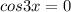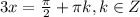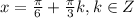
или
⇒ 
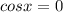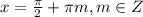
или
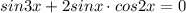
так как
⇒ 
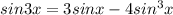
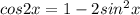
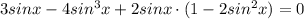
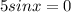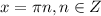
и
⇒ 
⇒ 
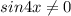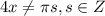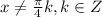
и
⇒ 
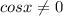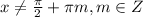
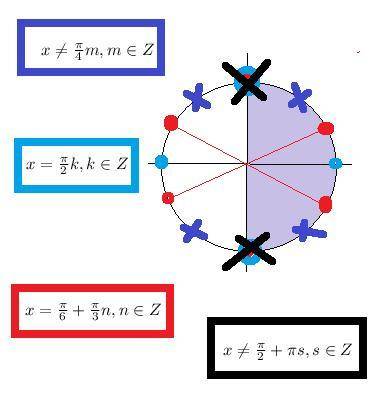
О т в е т второго случая c учетом cosx <0
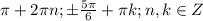( см. рис.2)
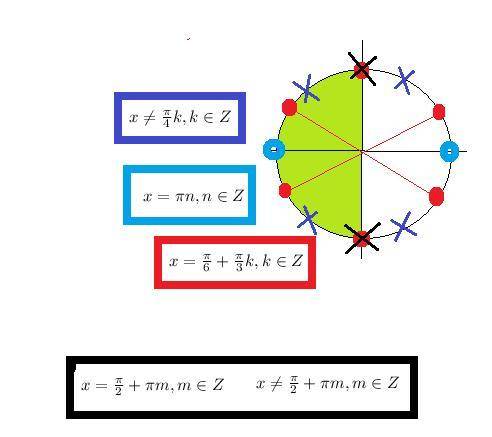
О т в е т. Объединяем ответы первого и второго случаев:
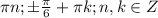
а) 5!=1*2*3*4*5=120
б)10!=3628800
в) 15! окончится тремя нулями
ноль на конце даёт 10 и сочетание 5 и 2