ответ:::::::::
Обьяснение:::::::
Можно эту задачу решить по формуле из физики (суть точно такая же как Вы и написали в условии). Формула такова: H=(gt(^2))/2 , то есть в числителе у нас "ж умножить на т в квадрате", а в знаменателе 2, где g-есть ускорение свободного падения(9,8 м/с(^2)), а t-это время, которое нам и нужно найти. Таким образом, из формулы выражаем величину t=sqrt(2H/g), где sqrt-корень, то есть величина 2Н/g находится под корнем. Считаем: t=sqrt(2*4410м/9,8м/с^2)=30секунд. Если вам нужно написать решение в тетрадь, то необязательно так всё расписывать, я писал так, чтобы вам было максимально понятно. В тетради же решение выглядеть должно так: H=(gt(^2))/2 сл-но t=sqrt(2H/g)=sqrt(2*4410м/9,8м/с^2)=30секунд.
Первый
(1,8 - 0,3y) * (2y + 9) = 0
(1,8 - 0,3y) = 0 (2y + 9) = 0
-0,3y = - 1,8 2y = -9
y = -1,8 : (-0,3) y = (-9) : 2
y = 6 y = -4,5
ответ: y₁ = -4,5; y₂ = 6.
Второй
(1,8 - 0,3y) * (2y + 9) = 0
3,6y + 16,2 - 0,6y² - 2,7y = 0
-0,6y² + 0,9y + 16,2 = 0
a = -0,6; b = 0,9; c = 16,2
D = b² - 4ac = 0,9² - 4 * (-0,6) * 16,2 = 0,81 + 38,88 = 39,69
Так как дискриминант больше нуля (D = 39,69), то уравнение имеет два корня:
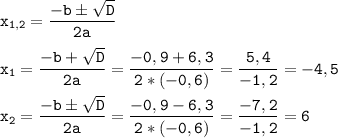
ответ: y₁ = -4,5; y₂ = 6.
х=64
Объяснение:
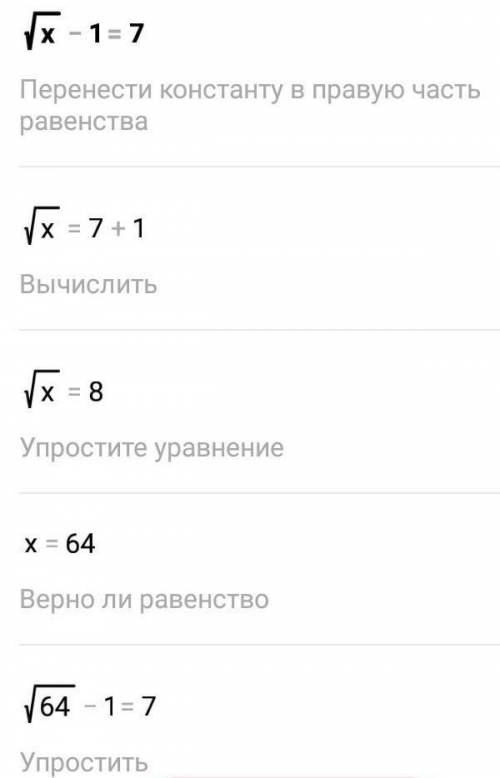
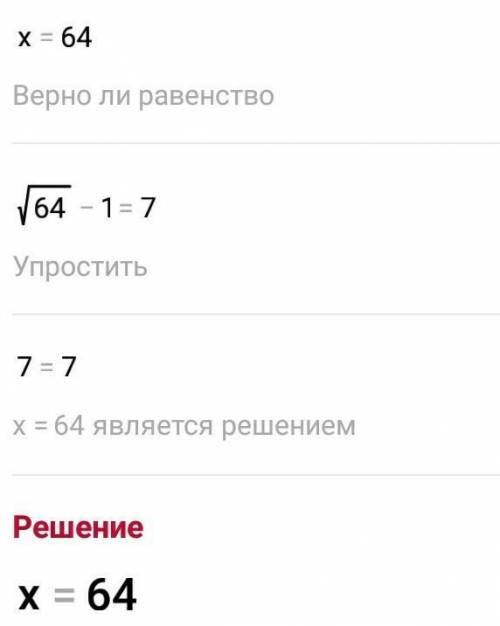
√х-1 =7
√х=8
(√х)^2=8^2
х=64