Рассмотрим вертикальные линии и горизонтальные. Каждую из них диагональ пересекает ровно один раз. При этом каждое пересечение вертикальной или горизонтальной линии соответствует пересечению двух (соседних) клеток. Посчитаем сумму вертикальных ( ) и горизонтальных клеток (
) и горизонтальных клеток (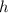 ): каждая клетка, которую пересекают (кроме двух крайних), считается дважды (она дважды участвует в паре), но также каждое пересечение считается дважды. Поэтому
): каждая клетка, которую пересекают (кроме двух крайних), считается дважды (она дважды участвует в паре), но также каждое пересечение считается дважды. Поэтому 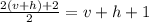 есть количество пересеченных клеток (мы добавили двойку в числителе вот почему: 2(v+h) - это удвоенное количество средних клеток (т.е. не крайних), а крайние посчитаны только один раз. Добавляя 2, мы считаем и крайние два раза. Теперь все клетки посчитаны дважды — можем делить на 2)
есть количество пересеченных клеток (мы добавили двойку в числителе вот почему: 2(v+h) - это удвоенное количество средних клеток (т.е. не крайних), а крайние посчитаны только один раз. Добавляя 2, мы считаем и крайние два раза. Теперь все клетки посчитаны дважды — можем делить на 2)
Пусть дан прямоугольник  , причем числа
, причем числа 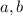 не имеют общих делителей (иначе какая-то клетка пересекалась бы по вершине — мы ее не считали). Тогда
не имеют общих делителей (иначе какая-то клетка пересекалась бы по вершине — мы ее не считали). Тогда 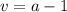 ,
, 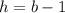 . Получаем
. Получаем 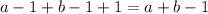 пересеченная клетка. Поскольку числа 239 и 566 не имеют общих делителей, к ним применима эта формула. Получаем, что диагональ пересекает 239+566-1=804 клетки
пересеченная клетка. Поскольку числа 239 и 566 не имеют общих делителей, к ним применима эта формула. Получаем, что диагональ пересекает 239+566-1=804 клетки
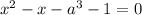 .
.
Уравнение - квадратное вида 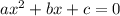 . Здесь
. Здесь 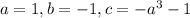 .
.
Чтобы уравнение имело корни нужно чтобы дискриминант был неотрицательным:  .
.
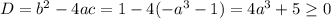
![4a^3\geq -5;\\\\a^3\geq -\frac{5}{4};\\\\ a\geq \sqrt[3]{\frac{-5}{4} } =-\frac{\sqrt[3]{5}\sqrt[3]{2}}{\sqrt[3]{8}}=-\frac{\sqrt[3]{10}}{2}](/tpl/images/1359/3684/7ecfd.png)
Если дискриминант равен 0 ( при ![a=-\frac{\sqrt[3]{10} }{2}](/tpl/images/1359/3684/650cc.png) ), то уравнение имеет единственное решение
), то уравнение имеет единственное решение 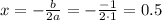 . Поскольку 0,5 > 0, значение параметра
. Поскольку 0,5 > 0, значение параметра ![a=-\frac{\sqrt[3]{10} }{2}](/tpl/images/1359/3684/650cc.png) пойдет в ответ.
пойдет в ответ.
Если дискриминант положителен (при ![a-\frac{\sqrt[3]{10} }{2}](/tpl/images/1359/3684/a9de6.png) ), то уравнение имеет 2 корня. Расписывать их необязательно.
), то уравнение имеет 2 корня. Расписывать их необязательно.
Чтобы ровно один корень из двух был положителен необходимо и достаточно того, чтобы произведение корней было отрицательным.
Если 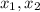 - корни уравнения, то по теореме Виета
- корни уравнения, то по теореме Виета 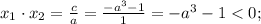
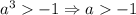
Нужно учесть, что должно также выполняться условие ![a-\frac{\sqrt[3]{10} }{2}](/tpl/images/1359/3684/a9de6.png) , так как в противном случае вещественных корней уравнение иметь не будет. Промежуток
, так как в противном случае вещественных корней уравнение иметь не будет. Промежуток ![(-\frac{\sqrt[3]{10} }{2}; +\infty)](/tpl/images/1359/3684/921c4.png) включает в себя промежуток
включает в себя промежуток 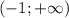 , поэтому все значения параметра
, поэтому все значения параметра 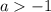 также пойдут в ответ.
также пойдут в ответ.
ОТВЕТ можно записать в двух видах: при ![a=-\frac{\sqrt[3]{10}}{2}](/tpl/images/1359/3684/f1e21.png) и
и 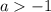 ; при
; при 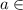 {
{![-\frac{\sqrt[3]{10}}{2}](/tpl/images/1359/3684/9e7d0.png) }
}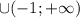 .
.
1) а1=-2 , d=3 , an=118-?
an=a1+(n-1)d
118= -2+(n-1)3
118= -2+3n-3
118 +5=3n
3n=123
n=41
a41=a1+40d= -2 + 120= 118 - является 41 членом арифметической прогрессии.
2) а39=83 ,d= -2 ,a1-?
a39=a1+ 38d
a1= a39 - 38d
a1= 83 - 38•(-2)=83 + 76=159
ответ: а1 = 159
3) а21= - 156, а34= -260, а1-? d-?
a21=a1 +20d --- a1=a21- 20d
a34=a1 +33d --- a1=a34- 33d
a1=a1
a21 -20d=a34 -33d
-20d+33d=a34-a21
13d= -260+156
13d=-104
d=-8
a1=a21-20d= -156-20•(-8)=-156+160= 4
ИЛИ:
а34=а1 + 33d
a34=a21+13d
a34-a21=13d
-260+156=13d
-104=13d
d=-8
a1=a34-33d=-260-33•(-8)=-260+264=4