а).
Просто подставляем в уравнение, задающее функцию,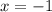 
:
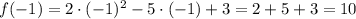
б).
Найдем те значения 
, при которых значение функции становится равным 
:
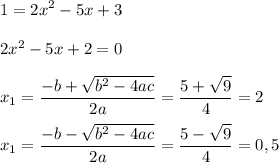
в).
Для того, чтобы определить, принадлежит ли точка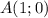 
графику, подставим в уравнение функци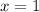и 
и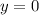 
, и посмотрим, что получится:
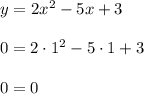
Получилось верное равенство! Значит, точка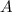 
действительно принадлежит графику рассматриваемой функции.
___________________________________________
Задание № 2.а).
Задача заключается в решении неравенства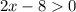 
:
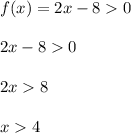
Получаем, что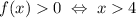 
, или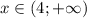 
.
б).
Ноли функции - это те значения , при которых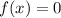 
:
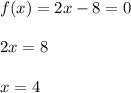
Значит, единственный ноль функции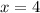 
.
___________________________________________
Задание № 3.а).
Область определения функции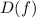 
- это те значения , при которых функция существует.
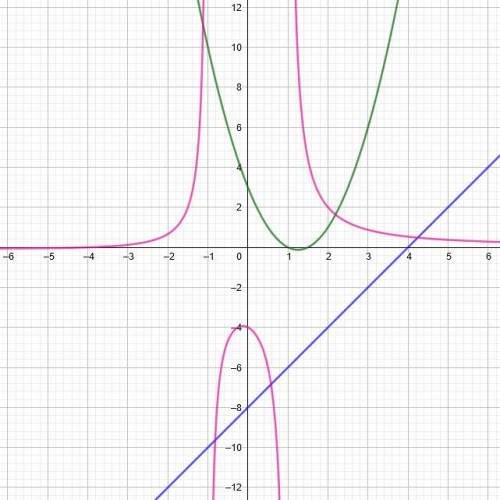
А функция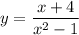 
существует только в том случае, если ее знаменатель не равен нолю:
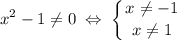
То есть, область определения данной функции - все действительные , кроме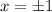 
:
Задача решена!
1848 375
Находим разность:
1848-375=1473
Теперь получили числа:
1473 375
Находим разность
1473-375=1098 и т.д:
1098-375=723
723-375=348
375-348=27
(ВНИМАНИЕ! Всегда от большего вычитаем меньшее - то есть нельзя вычитать 348-375 !)
348-27=321
321-27=294
294-27=267
267-27=240
240-27=213
213-27=186
186-27=159
159-27=132
132-27=105
105-27=78
78-27=51
51-27=24
27-24=3
24-3=21
21-3=18
18-3=15
15-3=12
12-3=9
9-3=6
6-3=3
Итак НОД=3
1848/3=616
375/3=125
Как видим, алгоритм Евклида довольно медленный.
Позже получили расширенный алгоритм Евклида, где монотонное вычитание заменили делением. Вычисление НОД расширенным алгоритмом значительно быстрее