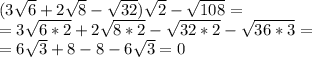
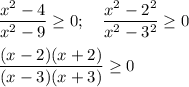
Решим неравенство методом интервалов.
Отмечаем на координатной прямой точки, в которых знаменатель и числитель обращаются в ноль. И выкалываем те, что из знаменателя. Мы получили 5 интервала. Перед дробью знак положительный и все множители имею пол. знак при х, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (все множители в нч степени - 1). Нас интересует, когда больше или равно, поэтому выбираем интервалы с плюсом, учитывая границы.
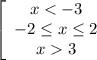
ответ: x ∈ (-∞;-3) ∪ [-2;2] ∪ (3;+∞).
В решении использовалась формула сокращённого умножения: a²-b²=(a-b)(a+b).

1. область определения х принадлежит (-бесконечность;+бесконечность).
2. пересечение с осью ординат (ОУ): x=0 f(x)=-1
3. исследование функции на четность/нечетность:
f(x)=x^3-2x^2+x-1
f(-x)=-x^3-2x^2-x-1 функция не является ни четной ни нечетной
4. производная функции:
3х^2-4x+1/
нули производной:
х=1/3. х=1.
5. Функция возрастает. х принадлежит (-беск.;1/3] U [1/3;+беск).
функция убывает. х принадлежит [1/3;1]
6. минимальное значение функции. -бесконечность
максимальное значение функции +бесконечность
(3корінь з 6+2корінь з 8-корінь з 32)корінь з 2-корінь з 108 = (3корінь з 6+2корінь з (4*2) -корінь з (4*4*2) )корінь з 2-корінь з 108= (3корінь з 6+2*2корінь з 2 - 4 корінь з 2 )корінь з 2-корінь з 108=(3корінь з 6+4корінь з 2 - 4 корінь з 2 )корінь з 2-корінь з 108= (3корінь з 6)* корінь з 2-корінь з 108= 3корінь з 6*2 - корінь з 12*9= 3корінь з 12 - 3корінь з 12=0