В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота СН. Угол НСВ равен 60 градусов, АН равен (10+k). Найдите длину отрезка АВ. Вместо K подставь свой порядковый номер по журналу.
1.Сделай рисунок к задаче.
2. Запиши свойства и теоремы, применяемые для решения этой задачи.
3.Правиьлно оформи задачу
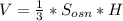
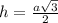
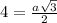
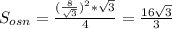
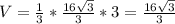
Sосн=a²√3/4, а - сторона правильного треугольника
по условию пирамида правильная треугольная, => основание высоты пирамиды - центр описанной около треугольника окружности - точка пересечения высот правильного треугольника, которые точкой пересечения делятся в отношении 2:1 считая от вершины.
прямоугольный треугольник:
гипотенуза с=5 см - длина бокового ребра правильной треугольной пирамиды
катет а=3 см - высота правильной пирамиды
катет b найти,
по теореме Пифагора: 5²=3²+b². b=4 см
b- (1/3) высоты правильного треугольника, которая вычисляется по формуле:
a=8/√3