ctgx(ctgx+1)=0
ctgx=0 или ctgx+1=0
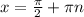ctgx=-1
n=-1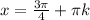 
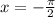k=-1
n=0 
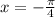
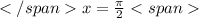k=0
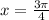
т.е. на данном промежутке находятся 4 корня
tg² x-tg x=0
tg x ( tg x - 1) = 0
1)
tg x = 0
x = pi*n n принадлежит z
на (-п/2;п) х = 0
2) tg x - 1 = 0
tg x = 1
x = pi/4 + pi*n n принадлежит z
на (-п/2;п) х =pi/4
ответ: 0, pi/4
ps
чтобы определить точки на (-п/2;п) можно нарисовать два круга : один положительный от 0 до 2pi, другой отрицательный от 0 до -2pi
на положительном круге интересуют точки на верхней полуокру жности те от 0 до pi, причем точка ноль принадлежит промежутку а пи нет.
на второй только точки четвертой четверти от 0 до -п/2, причем -п/2 не принадлежит отрезку.
на окружностях раставить точки из первого и второго ответа. те что попали в от 0 до pi и от 0 до -п/2 будут окончательным ответом.
Объяснение:
во втором надо "Z" заменить на "а", а "У"-на "b".