
Для начала разберемся с ОДЗ:
x + 6 > 0 ⇒ x > - 6
х + 6 ≠ 1 ⇒ х ⇒ - 5
x / (x-4) > 0
+ 0 - 4 +
_______⚪_________⚪_______
/////////////// ////////////////
x ∈ ( - ∞ ; 0 ) ∪ ( 4 ; + ∞)
Приступим:
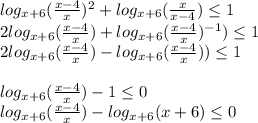
Дальше Необходимо вспомнить одну из формул рационализации:
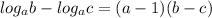
Тогда:
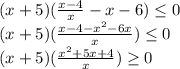
Приравняем к 0 и решим квадратное уравнение, дабы разложить эту часть на множители.
x² + 5x + 4 = 0
D = b² - 4ac = 9
x(1) = (-b-√D)/2a = - 4
x(2) = (-b+√D)/2a = - 1
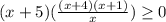
Воспользуемся методом интервалов:
+ -5 - -4 + -1 - 0 +
_____⚫______⚫______⚫______⚪_____________
////////// ////////////// /////////////////////
x ∈ ( - ∞ ; - 5] ∪ [ - 4 ; - 1 ] ∪ ( 0 ; + ∞)
Подставим под ОДЗ и получим ответ:
ответ: ( - 6 ; - 5] ∪ [ - 4 ; - 1 ] ∪ ( 4 ; + ∞)
Если уравнение имеет целые корни, то они являются делителями свободного члена. Методом пристального взгляда замечаем, что x = -1 обращает уравнение в верное числовое равенство. А это значит, что в разложении на линейные множители точно будет множитель (x + 1).
*тут должно было быть деление в столбик, но я не знаю, как его вставить сюда*
А дальше произведение равно нулю тогда, когда один из множителей равен нулю, а остальные существуют.
Откуда находим еще два решения: x = 2 и x = -0.5
ответ: x = -1, -0.5, 2