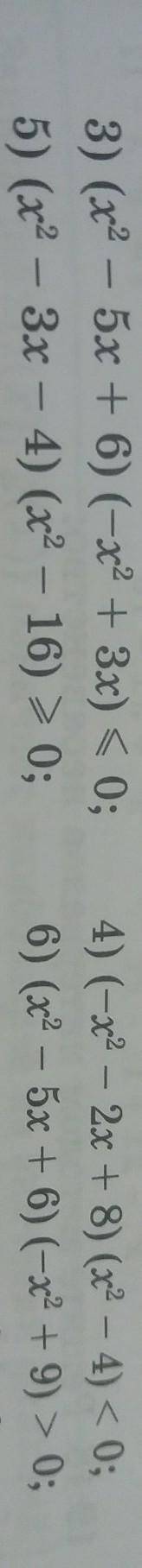
4ab+5b²;
при a=1; b=⅕ ответ: 1
Объяснение:
(a + 2b)²- (a - b)(b + a) = a²+ 4ab + 4b² - (a²- b²) = a² + 4ab + 4b² - a² +b²
взаимоуничтожаем a² и -a², приводим подобные члены и получаем: 4ab+5b²
при a=1; b=⅕ 4ab+5b²= 4×1×0,2 + 5×0,2² = 0,8 + 0,2 = 1
В выражении присутствуют формулы квадрат суммы и разность квадратов, раскрываем скобки, с учётом знаков перед скобкой, в данном случае "-", следовательно, все знаки внутри скобок меняем на противоположные. Потом взаимоуничтожаем a² и -a², приводим подобные члены и получаем 4ab+5b². Далее находим значение выражения 4ab+5b², при установленных значениях, для этого подставляем числа в полученное выражение и решаем.
cosx=a
3a²-5a-8=0
D=25+96=121
a1=(5-11)/6=-1⇒cosx=-1⇒x=π+2πn,n∈z
a2=(5+11)/6=2 2/3>1 нет решения
2)8cos^2x-14sinx+1=0
8-8sin²x-14sinx+1=0
sinx=a
8a²+14a-9=0
D=196+288=484
a1=(-14-22)/16=-2,25<-1 нет решения
a2=(-14+22)/16=1/2⇒sinx=1/2⇒x=(-1)^n*π/6+πn,n∈z
3)5sin^2x+14 sinxcosx+8cos^2x=0/cos²x
5tg²x+14tgx+8=0
tgx=a
5a²+14a+8=0
D=196-160=36
a1=(-14-6)/10=-2⇒tgx=-2⇒x=-arctg2+πn,n∈z
a2=(-14+6)/10=-0,8⇒tgx=-0,8⇒x=-arctg0,8+πk,k∈z
4)2tgx-9ctgx +3=0
2tgx-9/tgx+3=0
2tg²x+3tgx-9=0,tgx≠0
tgx=a
2a²+3a-9=0
D=9+72=81
a1=(-3-9)/4=-3⇒tgx=-3⇒x=-arctg3+πn,n∈z
a2=(-3+9)/4=1,5⇒tgx=1,5⇒x=arctg1,5+πk,k∈z
5)sin^2x-5cos^2x=2sin2x
sin²x-5cos²x-4sinxcosx=0/cos²x
tg²x-4tgx-5=0
tgx=a
a²-4a-5=0
a1+a2=4 U a1*a2=-5
a1=-1⇒tgx=-1⇒x=-π/4+πn,n∈z
a2=5⇒tgx=5⇒x=arctg5+πk,k∈z
6)5cos2x+5=8sin2x-6sin^2x
5cos²x-5sin²x+5sin²x+5cos²x-16sinxcosx+6sin²x=0/cos²x
6tg²x-16tgx+10=0
tgx=a
3a²-8a+5=0
D=64-60=4
a1=(8-2)/6=1⇒tgx=1⇒x=π/4+πn,n∈z
a2=(8+2)/6=5/3⇒tgx=5/3⇒x=arctg5/3+πk,k∈z