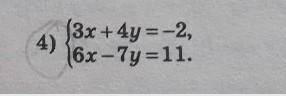
Эта задача была здесь на ответах уже несколько раз за последние сутки. Если у тебя продолжение такое:
и вернулся обратно через 6 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 3км/ч, а собственная скорость лодки 6 км/ч?
То вот тебе решение:
Расстояние от пристани до места рыбалки Х км
Скорость по течению 6 +3= 9км/час
Скорость против течения 6- 3 = 3 км/час
По течению плыл Х/6 часов
Против течения плыл Х/4 часов
Всего он плыл 6-2 = 4 часа (два часа сидел с удочкой)
Вот и простенькое уравнение:
Х/9 + Х/3= 4
4X = 36
Х = 9 км
4х - у = 9
3х + 7у = - 1
Система уравнений означает, что указанные равенства выполняются одновременно и равенство выполняется для одних и тех же переменных, в данном случае х и у.
Есть несколько решения систем уравнений, попробуем решить двумя
1. С подстановки.
4х - у = 9
3х + 7у = - 1
из первого уравнения:
у = 4х-9
подставим во второе уравнение
3х+7(4х-9)=-1
3х+28х=63-1
31х=62
х=2
у=4*2-9=-1
ответ: х=2; у=-1
Мы знаем, что уравнение сохранит справедливость, если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля.
Первое уравнение умножим на 7 (на 7 чтобы множители при у в 1 и 2 уравнениях оказались противоположными числами)
получается:
28х-7y=63
3х+7y=-1
Теперь сложим левые и правые части этих двух уравнений.
28х+3х=63-1
31х=62
х=2
находим y
4*2-y=9
8-y=9
y=-1
ответ: х=2; у=-1