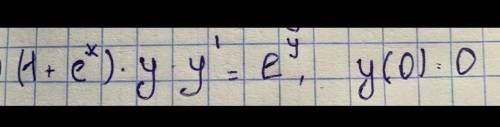
![(1+e^{x})\cdot y\cdot y'=e^{y}\ \ ,\ \ \ y(0)=0\\\\(1+e^{x})\cdot y\cdot \dfrac{dy}{dx}=e^{y}\\\\\int \dfrac{y\cdot dy}{e^{y}}=\int \dfrac{dx}{1+e^{x}}\\\\\\\int y\cdot e^{-y}\, dy=\Big[\ u=y\ ,\ dv=e^{-y}\, dy\ ,\ du=dy\ ,\ v=-e^{-y}\ \Big]=\\\\=uv-\int v\, du=-y\cdot e^{-y}+\int e^{-y}\, dy=-y\cdot e^{-y}-e^{-y}+C_1=-e^{-y}\cdot (y+1)+C_1\ ;\\\\\\\int \dfrac{dx}{1+e^{x}}=\Big[\ t=1+e^{x}\ ,\ e^{x}=t-1\ ,\ x=ln(t-1)\ ,\ dx=\dfrac{dt}{t-1}\ \Big]=](/tpl/images/1850/9256/c0c3f.png)
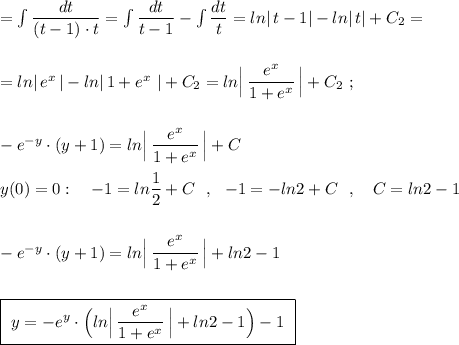
1)
Когда график пересекает ось абсцисс в какой-то точке, координаты этой точки (х;0), все точки лежащие на оси х имеют координату "ноль" по оси у. В итоге можем представить выражение следующим образом:
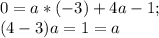
ответ: 1.
2)
Опять же в точке пересечения графика с абсциссой координаты по оси у это 0, значит: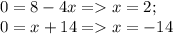 
ответ: 2 и -14.
3)
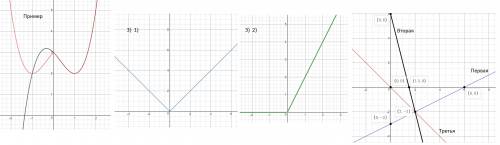
1) Можно раскрыть модуль по определению и увидеть, что получиться, а можно подумать. Есть какая-то функция, которая преобразует х в у (у=х), и отрицательные и положительные значения. А если взять модуль от х, то функция будет принимать те же значения для отрицательных значениях х, что и для положительных (когда они равны по модулю, пример -2 и 2), получается когда х будет отрицательным значения по оси х будут такими же, проще говоря всё чтобы справа (когда х положительный), отзеркалится влево по оси у. Покажу пример и другие графики внизу. То есть нам надо отразить график у=х как было сказано выше.
2) Тут уже по определению, но и всё просто:
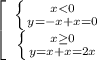
Два линейных уравнения.
4)
Если что-то пересекается в одной точке на координатной плоскости, то у них есть общие точки, то есть существует такая точка M--> (x₀;y₀), которая подходит есть в любой из функций, которые пересекаются в этой точке.
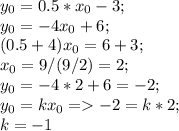
Теперь построение на общей координатной плоскости
Первая функция: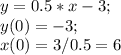 
Получили точки пересечения с осью у и х соответственно.
Вторая функция: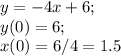 
Третья функция: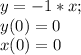 
ответ: -1.
