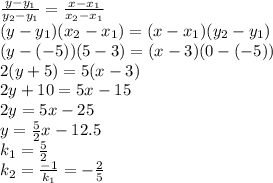
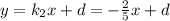
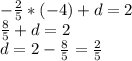
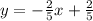
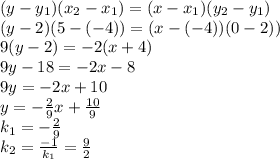
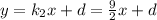
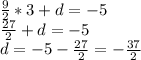
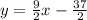
* * * * * * * * * * * * * * * * * * * *
Напишите уравнение касательной к графику функции f(x) = - x²+2x в точке x₀ = 2 .
ответ: y = - 2x + 4 .
Объяснение : Уравнение касательной к графику функции y=f(x) в точке x₀ имеет вид : y = f(x₀) + f '(x₀)* (x - x₀) .
f(x₀) = - x₀²+ 2x₀ ;
f ' (x) = (- x²+2x ) ' =(- x²) '+ (2x) ' = - (x²) '+ 2*(x) ' = - 2x +2 ;
f ' (x₀) = - 2x₀ + 2 ;
y = - x₀² + 2x₀ + (- 2x₀ + 2 ) * (x - x₀) . В данном примере x₀ = 2
следовательно : y = -2(x -2) ⇔ y = -2x + 4 .
у = f (2) + f '(2)*(x - 2) , где
f(2) = -2² +2*2 =0
f ' (2) = -2*2 +2 = - 2
у = -2(x - 2) ⇔ у = -2x + 4 || y =kx +b ||
Ну или, если не нравится перебор, системой уравнений. Пусть первая цифра - a, вторая цифра - b. Тогда наше число - это 10a+b. А обратное - 10b+a. Получаем систему уравнений:
{10b+a-36=10a+b
a+b=10}.
Отсюда:
{a=10-b;
10b+10-b-36=100-10b+b}
{a=10-b;
18b=126}
{a=10-b;
b=7}
a=3;b=7.