ответ: x = ±√3
Объяснение:
можно двумя решить (выбирайте-какой больше понравится...)
1) 3 = (√3)²
3*(х+2)² = (√3)² * (х+2)² = ( √3(х+2) )²
получили выражение вида: a² = b² --> |a| = |b| --> a = ±b
или 2х + 3 = √3*х + 2√3 --> 2x - √3*x = 2√3 - 3 --> x(2-√3) = √3(2-√3)
x = √3
или 2х + 3 = -√3*х - 2√3 --> 2x + √3*x = -2√3 - 3 --> x(2+√3) = -√3(2+√3)
x = -√3
2) т.к. х=-2 НЕ является решением уравнения (корнем) - это можно проверить устно: (-4+3)² ≠ 3*0²,
то обе части равенства можно разделить на (x+2)² ≠ 0
получим: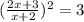 
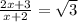или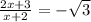 
продолжение решения аналогично 1)
или можно выделить целую часть:
--> 
--> 
--> 
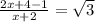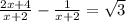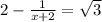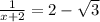
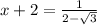
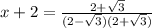
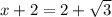--> x = √3 ( второе ("с минусом" -√3) аналогично)
8 y^2 - 7 y - 53 = 2 (4 y^2 - y + 1)
8 y^2 - 7 y - 53 = 8y^2 - 2y + 2
- 7 y - 53 = -2 y + 2
-5y =55
y = -11
Добавлю для некоторых подробное решение, с самого начала, без сокращений, с комментариями
(2y-3)(3y+1)+2(y-5)(y+5)=2(1-2y)^2+6y
Подробное решение
6y^2 + 2y - 9y - 3 + 2(y^2 - 25) = 2(1 - 4y + 4y^2) + 6y
6y^2 + 2y - 9y - 3 + 2y^2 - 50 = 2 - 8y + 8y^2 + 6y
8y^2 - 7y - 53 = 8y^2 - 2y + 2 /сокращаем 8y^2
-7y - 53 = -2y + 2 /Перенесём известные в одну сторону, неизвестные в другую
-7y + 2y = 2 + 53
-5y = 55
y = -11
y=-x^2-4x - графиком функции является парабола, ветви направлены вниз
m=-b/2a = 4/2 = -2
y=-(-2)^2+4*2=4
(-2;4) - координаты вершины параболы
y=4+x - прямая, проходящая через точки (0;4), (-4;0)
Знайдемо обмежені лінії
\begin{gathered}-x^2-4x=4+x\\ x^2+5x+4=0\end{gathered}−x2−4x=4+xx2+5x+4=0
За т. Вієта: x_1=-1;\,\,\,\, x_2=-4x1=−1;x2=−4
Знайдемо площу фігури
\begin{gathered}\displaystyle \int\limits^{-1}_{-4} {(-x^2-4x-(4+x))} \, dx = \int\limits^{-1}_{-4} {(-x^2-5x-4)} \, dx =\\ \\ \\ =\bigg(- \frac{x^3}{3} - \frac{5x^2}{2}-4x\bigg)\bigg|^{-1}_{-4}= \frac{1}{3} - \frac{5}{2} +4- \frac{4^3}{3} + \frac{5\cdot4^2}{2} -16=4.5\end{gathered}−4∫−1(−x2−4x−(4+x))dx=−4∫−1(−x2−5x−4)dx==(−3x3−25x2−4x)∣∣∣∣∣−4−1=31−25+4−343+25⋅42−16=4.5
Объяснение:
Это