Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
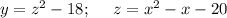
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
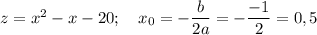 - координата вершины
- координата вершины
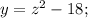 z = 0 - координата вершины параболы
z = 0 - координата вершины параболы

x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
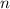 равных частей
равных частей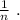
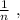 нужно разрезать верёвочку длины 2 на
нужно разрезать верёвочку длины 2 на  частей.
частей.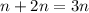 частей.
частей.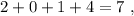 не делится на три.
не делится на три.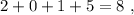 не делится на три.
не делится на три.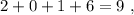 делится на три!
делится на три!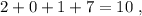 не делится на три.
не делится на три. не делится на три.
не делится на три.
б) 2с(с во второй+3с-1)=2с в третей степени+5с во торой степени-1
в) (3а-5)(4а-3)=7а во второй степени-6а-20а-6а...6а зачеркиваем, так как подобные...=7а во второй -20а