
В решении.
Объяснение:
Решить графически систему уравнений:
х + у = 9
х - у = 1
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Прежде преобразовать уравнения в уравнения функций:
х + у = 9 х - у = 1
у = 9 - х -у = 1 - х
у = х - 1
Таблицы:
х -1 0 1 х -1 0 1
у 10 9 8 у -2 -1 0
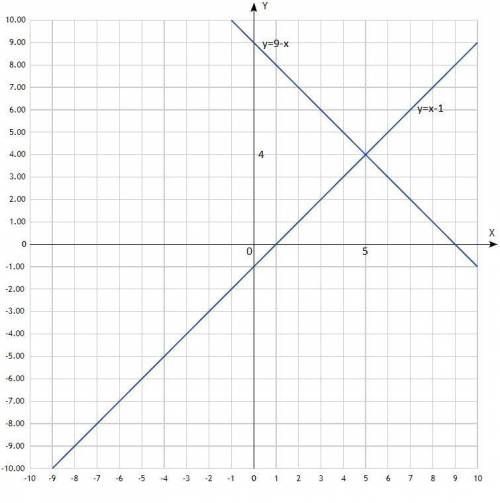
По вычисленным точкам построить прямые.
Согласно графиков, координаты точки пересечения прямых: (5; 4).
Решение системы уравнений: (5; 4).
смотрите, косинус "болтается" между 1 и -1. поэтому y будет "болтаться" между (1/2 -1) и (-1/2 -1), то есть между -1/2 и -3/2.
Период у косинуса от 2х будет pi - ясно, что 2х при этом меняются на 2pi. "Первый" максимум будет на (-pi/6), следующий (5*pi/6), между ними минимум на pi/3. Точки, когда он пересекает среднюю линюю y = -1, будут pi/12 и 7*pi/12.
Вообще лучше сначала сжать, а потом сдвигать.
y=(1/2)*cos(2*(x+pi/6)) - 1 можно так записать
y1=(1/2)cos(2*x1), где y1 = y +1; x1 = x + pi/6;
В осях x1 y1 как раз сжимаем, а потом все сдвигаем по х на pi/6 влево и по y на 1 вниз. Это нагляднее :))
Объяснение:
надеюсь .=).......