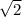 (sin2x + sinx) -2cosx
(sin2x + sinx) -2cosx 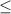 1 , если x ∈ [0; π]
1 , если x ∈ [0; π]![\sqrt2(sin2x+sinx)-2cosx\leq 1\ \ ,\ \ \ x\in [\ 0\ ;\ \pi \ ]\\\\\sqrt2\cdot 2sinx\cdot cosx+\sqrt2sinx-2cosx-1\leq 0\\\\\sqrt2sinx\cdot (2cosx+1)-(2cosx+1)\leq 0\\\\(2cosx+1)(\sqrt2sinx-1)\leq 0\\\\a)\ \ \left\{\begin{array}{l}2cosx+1\leq 0\\\sqrt2sinx-1\geq 0\end{array}\right\ \ \ ili\ \ \ b)\ \ \left\{\begin{array}{l}2cosx+1\geq 0\\\sqrt2sinx-1\leq 0\end{array}\right](/tpl/images/2095/7176/fd529.png)
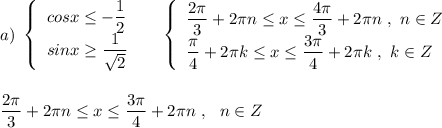
![c)\ \ x\in \Big[-\dfrac{2\pi }{3}+2\pi n\ ;\ \dfrac{\pi}{4}+2\pi n\ \Big]\cup \Big[\ \dfrac{2\pi }{3}+2\pi n\ ;\ \dfrac{3\pi }{4}+2\pi n\ \Big]\ \ ,\ n\in Z\ -\ otvet\\\\\\d)\ \ x\in [\ 0\ ;\ \pi \ ]:\ \ x\in \Big[\ 0\ ;\, \dfrac{\pi}{4}\ \Big]\cup \Big[\ \dfrac{2\pi }{3}\ ;\ \dfrac{3\pi }{4}\ \Big]](/tpl/images/2095/7176/f66b0.png)
![(sin2x + sinx) -2cosx 1 , если x ∈ [0; π]](/tpl/images/2095/7176/1507c.jpg)
В решении.
Объяснение:
При каких значениях x трёхчлен 2x²−7x+6 принимает отрицательные значения?
2x²−7x+6 < 0
Приравнять к нулю и решить как квадратное уравнение:
2x²−7x+6 = 0
D=b²-4ac =49-48=1 √D=1
х₁=(-b-√D)/2a
х₁=(7-1)/4
х₁=6/4
х₁=1,5;
х₂=(-b+√D)/2a
х₂=(7+1)/4
х₂=8/4
х₂=2.
Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= 1,5 и х= 2, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у < 0 (как в неравенстве), при значениях х от 1,5 до 2, то есть, решения неравенства находятся в интервале
х∈ (1,5; 2), или 1,5 < x < 2.
Неравенство строгое, скобки круглые.
Верный ответ самый последний.