X/ x-3-2/ x+3= 4x²-9 a) укажите область допустимых значений уравнения
f) Приведите рациональное уравнение к квадратному уравнению
с) Найдите решение рационального уравнения

УМОЛЯЮ

X/ x-3-2/ x+3= 4x²-9 a) укажите область допустимых значений уравненияf) Приведите рациональное уравн

👇

Открыть все ответы

Ответ:

annayotubeanna

05.10.2020

1) 4b(b+9)-3(b+12b)-b+7 = b+7
4b² + 36b - 3b - 36b - b + 7 - b - 7 =0
4b² - 5b = 0
b(4b - 5) = 0
b1 = 0
b2 = 5/4 = 1.25
2) 4b(b+9)-3(b+12b)-b+7 = 0
4b² + 36b - 3b - 36b -b +7 = 0
4b² - 4b +7 = 0
4b(b-1) + 7 =0
1. 4b + 7 =0
4b = -7
b1 = -1.75
2. b - 1 + 7 = 0
b +6 =0
b2 = -6
3) 4b(b+9)-3(b+12b)-b+7 = 7
4b² + 36b - 3b - 36b -b +7 - 7 = 0
4b² - 4b =0
4b (b - 1) = 0
b1 = 0
b2 = 1
4) 4b(b+9)-3(b+12b)-b+7 = 5
4b² + 36b - 3b - 36b -b +7 - 5 =0
4b² - 4b + 2 =0
2b² - 2b + 1 = 0
2b (b - 1) +1 = 0
1. 2b +1 = 0
b1 = -0.5
2. b - 1 + 1 =0
b2 = 0

4,7(17 оценок)

Ответ:

milankae

05.10.2020

выпишем координаты данных векторов:

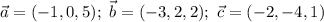
$\vec{a}=(-1,0,5);\ \vec{b}=(-3,2,2);\ \vec{c}=(-2,-4,1)$

координаты:

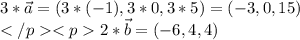
$3*\vec{a}=(3*(-1),3*0,3*5)=(-3,0,15)\\2*\vec{b}=(-6,4,4)$

скалярное произведение векторов - число:

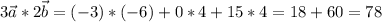
$3\vec{a}*2\vec{b}=(-3)*(-6)+0*4+15*4=18+60=78$

б)

координаты:

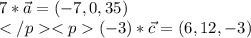
$7*\vec{a}=(-7,0,35)\\(-3)*\vec{c}=(6,12,-3)$

векторное произведение векторов - вектор, находим его координаты:

$7\vec{a}\times (-3\vec{b})=\left|\begin{array}{ccc}\vec{i} & \vec{j} & \vec{k} \\-7 & 0 & 35 \\6 & 12 & -3\end{array}\right|=\vec{i}*\left|\begin{array}{cc}0 & 35 \\12 & -3\end{array}\right|-\vec{j}*\left|\begin{array}{cc}-7 & 35 \\6 & -3\end{array}\right|+\vec{k}*\left|\begin{array}{cc}-7 & 0 \\6 & 12\end{array}\right|=\vec{i}*(-12*35)-\vec{j}*(21-6*35)+\vec{k}*(12*(-7))=\\=-420\vec{i}+189\vec{j}-84*\vec{k}=(-420,189,-84)$

находим модуль(длину) полученного вектора:

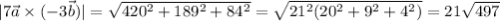
$|7\vec{a}\times (-3\vec{b})|=\sqrt{420^2+189^2+84^2}=\sqrt{21^2(20^2+9^2+4^2)}=21\sqrt{497}$

в)

координаты:

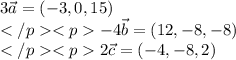
$3\vec{a}=(-3,0,15)\\-4\vec{b}=(12,-8,-8)\\2\vec{c}=(-4,-8,2)$

смешанное произведение векторов - число, находим его:

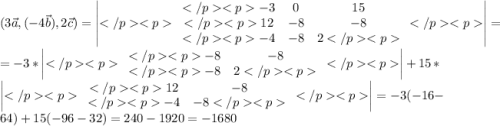
$(3\vec{a},(-4\vec{b}),2\vec{c})=\left|\begin{array}{ccc}-3 & 0 & 15 \\12 & -8 & -8 \\-4 & -8 & 2\end{array}\right|=\\=-3*\left|\begin{array}{cc}-8 & -8 \\-8 & 2\end{array}\right|+15*\left|\begin{array}{cc}12 & -8 \\-4 & -8\end{array}\right|=-3(-16-64)+15(-96-32)=240-1920=-1680$

г)

Координаты:

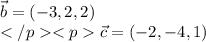
$\vec{b}=(-3,2,2)\\\vec{c}=(-2,-4,1)$

Векторы коллинеарны, если их соответствующие кординаты пропорциональны

Проверим это утверждение:

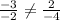
$\frac{-3}{-2}\neq \frac{2}{-4}$

Данное равенство неверно, значит векторы b и c не коллинеарны

Векторы ортогональны, если их скалярное произведение равно нулю.

Проверим это утверждение:

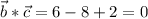
$\vec{b}*\vec{c}=6-8+2=0$

- верно, значит данные векторы ортогональны

Векторы b и c ортогональны

д)

Координаты:

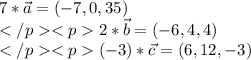
$7*\vec{a}=(-7,0,35)\\2*\vec{b}=(-6,4,4)\\(-3)*\vec{c}=(6,12,-3)$

Три вектора компланарны, если их смешанное произведение равно нулю.

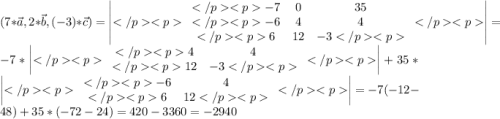
$(7*\vec{a},2*\vec{b},(-3)*\vec{c})=\left|\begin{array}{ccc}-7 & 0 & 35 \\-6 & 4 & 4 \\6 & 12 & -3\end{array}\right|=-7*\left|\begin{array}{cc}4 & 4 \\12 & -3\end{array}\right|+35*\left|\begin{array}{cc}-6 & 4 \\6 & 12\end{array}\right|=-7(-12-48)+35*(-72-24)=420-3360=-2940$